Градиентные методы. Используя градиентные методы, можно найти, решение любой задачи нелинейного программирования

Используя градиентные методы, можно найти, решение любой задачи нелинейного программирования. Применение этих методов в общем случае позволяет найти точку локального экстремума. Поэтому более целесообразно использовать их для нахождения решения задач выпуклого программирова­ния. Процесс нахождения решения задачи с помощью градиентных методов состоит в том, что начиная с некоторой точки осуществляется последо­вательный переход к некоторым другим точкам до тех пор, пока не будет найдено приемлемое решение исходной задачи. Градиентные методы могут быть подразделены на две группы.

К первой группе относятся методы, при использовании которых иссле­дуемые точки не выходят за пределы области допустимых решений задачи. В данном случае наиболее распространенным является метод Франка - Вульфа. Ко второй - методы, при использовании которых исследуемые точки могут как принадлежать, так и не принадлежать области допустимых решений. Од­нако в результате реализации итерационного процесса находится точка об­ласти допустимых решений, определяющая приемлемое решение. Наиболее часто используются метод штрафных функций и метод Эрроу - Гурвица. При нахождении решения задачи градиентными методами ите­рационный процесс продолжается до тех пор, пока градиент функции 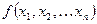в очередной точке не станет равным нулю или же пока не выполнится неравенство

, где (точность полученного решения).

Метод Франка - Вульфа. Пусть требуется найти максимальное значе­ние вогнутой функции

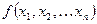(9)

при условиях

(10)

(11)

Ограничения содержат только линейные неравенства. Эта особенность является основой для замены в окрестности исследуемой точки нелинейной целевой функции линейной, в результате чего решение исходной задачи сво­дится к последовательному решению задач линейного программирования.

Процесс нахождения решения начинают с определения точки, принад­лежащей области допустимых решений. Пусть это точка . Вычисляют в этой точке градиент функции (9):

,

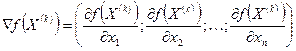строят линейную функцию

. (12)

Находят максимум функции (12) при ограничениях (10) и (11). Пусть решение данной задачи определяется точкой . За новое допустимое решение исходной задачи принимают координаты точки , которые находят по формулам

,

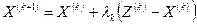где - некоторое число, называемое шагом вычислений . За принимают наименьший корень уравнения или выбирают произвольно, если он не принадлежит интервалу (0; 1).

Метод штрафных функций. Рассмотрим задачу нелинейного программирования (6) -(8), где - выпуклые функции.

Вместо того, чтобы решать эту задачу, находят максимум функции

,

где определяется системой ограничений и называется штрафной функцией. Последнюю можно построить различными способами. Наиболее часто она имеет вид

,

где

а - некоторые постоянные числа, представляющие собой весовые ко­эффициенты.

Используя штрафную функцию, последовательно переходят от одной точки к другой до тех пор, пока не получат приемлемое решение. Координаты последующей точки находят по формуле

,

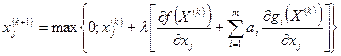где - шаг вычислений .

Итерационный процесс обычно начинают при сравнительно малых зна­чениях и, продолжая его, эти значения постепенно увеличивают.

Метод Эрроу - Гурвица. При нахождении решения задачи нелинейно­го программирования методом штрафных функций значения , выбирают произвольно, что приводит к значительным колебаниям удаленности опреде­ляемых точек от области допустимых решений. Этот недостаток устраняется при решении задачи методом Эрроу - Гурвица, согласно которому на оче­редном шаге числа 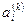находят по формуле

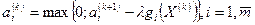
В качестве начальных значений 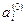берут произвольные неотрицательные числа.

Поиск по сайту: