АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Матрица графов

Читайте также:
  1. Nikon D7100 - матрица APS-C в идеальном оформлении
  2. SWOT- матрица
  3. V2: ДЕ 4 – Линейные отображения. Линейные операции над матрицами
  4. Анализ матричных данных (матрица приоритетов)
  5. Б1 2. Линейный оператор в конечномероном пространстве, его матрица. Характеристический многочлен линейного оператора. Собственные числа и собств векторы.
  6. Билет 11. Различные уравнения прямой в пространстве. Матрица перехода к новому базису.
  7. Билет 13. Линейные операторы. Матрица линейного оператора.
  8. Билет 23. Матрица SWOT – анализа.
  9. Билет 27 Ортогональный оператор и его матрица в ортонормированном базисе
  10. Билет 27. Жорданов базис и жорданова матрица линейного оператора в комплексном пространстве.
  11. Билет 32. Сопряженный оператор. Существование и единственность. Матрица сопряженного оператора.
  12. Билет26 Самосопряженный оператор и его матрица в ортонормированном базисе.

 

Граф может быть задан разными способами: рисунком, перечислением вершин и ребер (или дуг) и т. д. Одним из самых удобных способов является задание графа с помощью матрицы. Пусть некоторый граф G имеет п вер­шин и т ребер . Построим матрицу, имею­щую п строк и т столбцов. Каждая строка матрицы будет соответствовать вершине, а столбец - ребру графа. В столбце 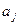все элементы, кроме двух, будут равны нулю. Для ориентированного графа в строке, соответствующей начальной вершине дуги 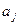, ставят число +1, а в строке, соответствующей конечной вершине, - число -1. Для неориентированного графа в строках матрицы, соответствующих концевым вершинам ребра 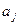, ставят 1, а в ос­тальных строках - 0. Построенные матрицы называются матрицами инциденций графа.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)