Квадратичное программирование

Задачи квадратичного программирования имеют следующие особенности: целевая функция представляет собой сумму вида 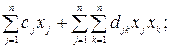функции, входящие в ограничения, линейны относительно х_j, т.е. 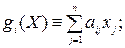обычно присутствует требование неотрицательности переменных.

Структура задач квадратичного программирования позволяет широко использовать теорию Куна - Таккера для поиска оптимальных решений. Различные интерпре­тации необходимых условий существования экстремума (4) (п. 4.4) привели к разработке целого ряда алгоритмов, многие из которых преследуют цель свести решение исход­ной квадратичной задачи к вариантам линейного про­граммирования. Что касается достаточных условий экс­тремума, то в данном случае они выражены в требовании выпуклости (вогнутости) функции 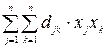. Можно показать, что рассматриваемая квадра­тичная форма обладает свойством выпуклости (вверх), если она является неположительно (или отрицательно) определенной в U, т.е. 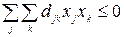для всех х_j, x_k, удовлетворяющих принятым ограничениям.

Учитывая сказанное, обратимся к задаче: найти

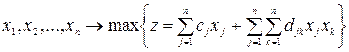при

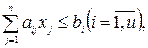
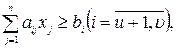(5)

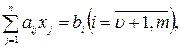
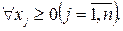
Положив 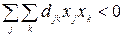, говорить в дальней­шем только о глобальном экстремуме z..

Рассмотрим необходимые условия существования X*, z*. Здесь

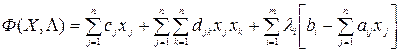
и

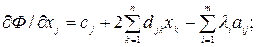
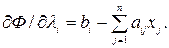
Обозначим для удобства через p_j - производную 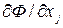, а через производную q_i - 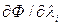. Тогда искомые условия можно трактовать так: значения 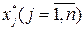определяются теми решениями системы

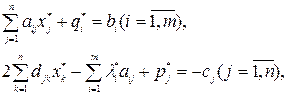(6)

которые удовлетворяют требованиям

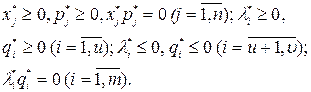
Переход к системе (6) позволяет в большинстве случаев упростить процедуру отыскания 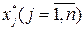за счёт использования симплекс-алгоритма. Возвращаясь к (6), заметим, что рассма­триваемая система содержит т+п линейных уравнений с 2(n+m) неизвестными 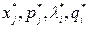. Предполагая уравнения (6) независимыми (поскольку независимы условия, из которых они получены), можно сказать, что п+т из названных 2(п+т) переменных являются свободными.

Если некоторое решение (6) удовлетворяет требованиям

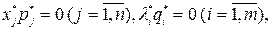
то среди его компонент должно быть как минимум п+т равных нулю; таким образом, оно может иметь вид «ровно п+т компонент отличны от нуля, ровно п+т компонент равны нулю» или «менее п+т компонент отличны от нуля, более п+т компонент равны нулю».

Очевидно, подобные решения являются базисными, и для отыскания X* должен существовать метод, аналогичный симплекс-методу, оперирующему с базис­ными решениями. Возникает вопрос: нельзя ли сразу, вы­брать произвольно п+т свободных переменных среди 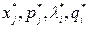положить их равными нулю, а затем определить через них остальные переменные в соответ­ствии, с уравнениями (6)? Ответ, здесь может быть только отрицательным, потому что произвольный выбор решения может привести к нарушению условий 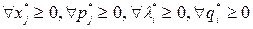. Приходится обращаться к специальным методам определения 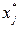. Одним из них является так называемый метод Вольфа, предусматривающий исследование задач линейного про­граммирования с целью получить решения задачи квад­ратичного программирования.

Поиск по сайту: