 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Простейшие экономические задачи, решаемые методом динамического программирования
Задача распределения капиталовложений:
Планируется распределение начальной суммы средств  между п предприятиями
между п предприятиями  . Предполагается, что выделенные предприятию
. Предполагается, что выделенные предприятию  в начале планового периода средства
в начале планового периода средства  приносят доход
приносят доход 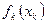
 . Будем считать, что:
. Будем считать, что:
1) доход, полученный от вложения средств в предприятие  , не зависит от вложения средств в другие предприятия;
, не зависит от вложения средств в другие предприятия;
2) доход, полученный от разных предприятий, выражается в одинаковых единицах;
3) общий доход равен сумме доходов, полученных от всех средств, вложенных во все предприятия.
Математическая модель задачи следующая:

при ограничениях
 ,
,
 .
.
Опишем задачу в виде модели динамического программирования.
За номер k -гошага примем номер предприятия, которому выделяются средства  . Уравнениями состояния служат равенства
. Уравнениями состояния служат равенства

 .
.
Суммарный доход за п шагов составит

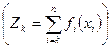 .
.
Уравнения Беллмана имеют вид
 ;
;
 .
.
Задача календарного планирования трудовых ресурсов:
Предпринимателю необходимо составить план регулирования численности рабочих на последующие пять недель. Он оценивает минимальные потребности в рабочей силе bi на каждую из пяти недель следующим образом: 5, 7, 8, 4 и 6 рабочих для i = 1, 2, 3, 4 и 5 соответственно. Предприниматель имеет возможность регулировать количество имеющихся в наличии рабочих путем найма и увольнения. Пусть yj - количество рабочих, имеющихся в наличии на j -й неделе. Определим  как величину убытков, связанных с тем, что yj превышает заданное значение bj, a
как величину убытков, связанных с тем, что yj превышает заданное значение bj, a 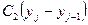 -как величину накладных расходов по найму новых рабочих
-как величину накладных расходов по найму новых рабочих  .Необходимо составить оптимальный план регулирования численности рабочих для 5-недельного периода планирования при условии, что исходное количество
.Необходимо составить оптимальный план регулирования численности рабочих для 5-недельного периода планирования при условии, что исходное количество 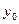 рабочих, имеющихся в наличии к началу первой недели, составляет пять человек. Опишем задачу в виде модели динамического программирования.
рабочих, имеющихся в наличии к началу первой недели, составляет пять человек. Опишем задачу в виде модели динамического программирования.
Этап j ставится в соответствие j -й неделе. Состояние  на этапе j выражает количество рабочих, имеющихся к концу этапа j-1. Варианты решения yj описываются количеством рабочих, имеющихся на этапе j. Обозначим через
на этапе j выражает количество рабочих, имеющихся к концу этапа j-1. Варианты решения yj описываются количеством рабочих, имеющихся на этапе j. Обозначим через  минимальную величину расходов, осуществленных в течении периодов времени (недель) j,j+1,…,5, при заданном yj-1. Рекуррентное соотношение записывается в следующем:
минимальную величину расходов, осуществленных в течении периодов времени (недель) j,j+1,…,5, при заданном yj-1. Рекуррентное соотношение записывается в следующем:
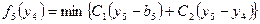 ;
;

Задача о загрузке самолёта:
Пусть имеется самолет грузоподъемностью W и его следует загрузить предметами n - различных типов и различные ценности. Необходимо загрузить самолет предметами максимальной ценности, если известно, что 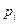 - вес предмета
- вес предмета  -го типа
-го типа  ,
,  - стоимость предмета
- стоимость предмета  -го типа,
-го типа,  число предметов
число предметов  -го типа.
-го типа.
Составим математическую модель задачи

при ограничениях


Если снять условие целочисленности, то это задача линейного программирования. Решим задачу, считая W - величиной произвольной. Если загрузить самолет только предметами 1-го типа, то максимальная стоимость груза

при ограничениях
 .
.
Число предметов 1-го типа  . Пусть
. Пусть 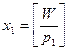 , тогда
, тогда  .
.
Пусть в самолет загружают предметы 1-го и 2-го типов. Обозначим максимальную стоимость через  . Если было загружено
. Если было загружено  предметов 2-го типа, то вес предметов 1-го типа не должен превышать
предметов 2-го типа, то вес предметов 1-го типа не должен превышать  , их стоимость соответственно равна
, их стоимость соответственно равна  и
и  . Тогда
. Тогда

Продолжая процесс, то есть предметы новых типов через n - шагов приходим к соотношению

где  - максимальная стоимость груза, состоящего из предметов n типов,
- максимальная стоимость груза, состоящего из предметов n типов,  - стоимость предметов n -го типа;
- стоимость предметов n -го типа;  - максимальная стоимость груза, состоящего из предметов (n-1) типов, общий вес которых не более
- максимальная стоимость груза, состоящего из предметов (n-1) типов, общий вес которых не более  .
.
Поиск по сайту: