 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Возможные обобщения метода множителей. Седловая точка функции Лагранжа
Здесь будут обсуждены вопросы относящиеся к оптимизационным задачам, содержащим ограничения вида  и
и 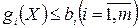 . Главное внимание уделяется изучению особенностей функции Лагранжа
. Главное внимание уделяется изучению особенностей функции Лагранжа  и связанных с ними условий существования экстремума.
и связанных с ними условий существования экстремума.
Введем определение: точка  , заданная своими координатами
, заданная своими координатами  , является седловой, для функции
, является седловой, для функции  , если неравенства
, если неравенства  выполнены для всех
выполнены для всех  из некоторой окрестности
из некоторой окрестности  .
.
Это определение относится к локальной седловой точке, поскольку требование выполнить указанные в нем неравенства связано лишь с теми  , которые находятся «вблизи»
, которые находятся «вблизи»  . В том же смысле можно говорить и обо всех
. В том же смысле можно говорить и обо всех  , представляющих интерес в той или иной задаче; соответствующая седловая точка рассматривается как глобальная.
, представляющих интерес в той или иной задаче; соответствующая седловая точка рассматривается как глобальная.
Анализ необходимых условий существования таких точек будет проведен в предположении, что часть переменных  не имеет ограничения на знак, остальные же должны быть либо неотрицательными, либо неположительными; для конкретности
не имеет ограничения на знак, остальные же должны быть либо неотрицательными, либо неположительными; для конкретности  при
при  и
и 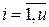 ;
;  при
при  и
и 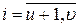 ; произвольный знак имеют хi и λi при
; произвольный знак имеют хi и λi при  ,
,  .
.
Пусть точка  является седловой для
является седловой для  . Рассмотрим две группы производных, считая, что таковые существуют:
. Рассмотрим две группы производных, считая, что таковые существуют:  . Поскольку
. Поскольку  определена как точка максимума Ф по X и минимума по
определена как точка максимума Ф по X и минимума по 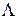 , производные
, производные  ,должны обратиться в нуль при
,должны обратиться в нуль при  , если нет ограничений на знак этих
, если нет ограничений на знак этих  .
.
Таким образом,  для
для  и
и  для
для  .
.
Чтобы понять, как ведут себя рассматриваемые производные при  , достаточно выбрать переменную хк с номером
, достаточно выбрать переменную хк с номером  ипровести на ее примере необходимое исследование, cчитая все остальные переменные фиксированными.
ипровести на ее примере необходимое исследование, cчитая все остальные переменные фиксированными.
Если  как функция только хк достигает максимума при
как функция только хк достигает максимума при  , то
, то 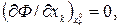 ; но если
; но если  (точка максимума Ф принадлежит границе области хк
(точка максимума Ф принадлежит границе области хк  0), то можно ожидать либо
0), то можно ожидать либо 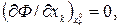 либо
либо  (рис. 7). Повторив подобные рассуждения применительно к другим
(рис. 7). Повторив подобные рассуждения применительно к другим  нетрудно получить сводку необходимых условий существования
нетрудно получить сводку необходимых условий существования  .
.

 (1)
(1)
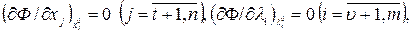
причем всегда 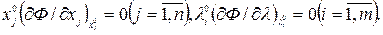


Рис. 7 Рис. 8
Для анализа, достаточных условий введем определение: некоторая функция F(X) называется выпуклой на интервале [ Х1,Х2 ], если 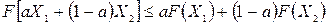 при 0<a<1 (рис. 8). В основе определения вогнутой на [ Х1, Х2 ] функции лежит неравенство противоположного смысла, причем часто употребляются термины «выпуклая вниз», «выпуклая вверх».
при 0<a<1 (рис. 8). В основе определения вогнутой на [ Х1, Х2 ] функции лежит неравенство противоположного смысла, причем часто употребляются термины «выпуклая вниз», «выпуклая вверх».
Пусть Ф(Х, 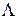 ) является выпуклой (вверх) по X для всех X из
) является выпуклой (вверх) по X для всех X из  -окрестности Х0, т.е.
-окрестности Х0, т.е.
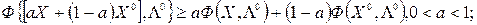
это значит  . Выбирая
. Выбирая  таким, что
таким, что  (сохраняются линейные члены разложения в ряд Тейлора), получаем
(сохраняются линейные члены разложения в ряд Тейлора), получаем
 или
или  .
.
Слагаемое 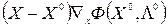 интерпретируется, очевидно, как
интерпретируется, очевидно, как

Если, все эти соотношения рассматриваются при выполненных условиях (1), то,

Следовательно,  - неположительная величина и тем более
- неположительная величина и тем более  . Таким образом, из (1) и предположения о выпуклости вверх
. Таким образом, из (1) и предположения о выпуклости вверх  но X получено неравенство, присутствующее в определении седловой точки.
но X получено неравенство, присутствующее в определении седловой точки.
Считая теперь  выпуклой (вниз) по
выпуклой (вниз) по 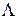 вблизи
вблизи  , т.е.
, т.е.  при
при  , нетрудно придти к выводу:
, нетрудно придти к выводу:  . Этим подтверждается достаточность общих условий (1) и требования «
. Этим подтверждается достаточность общих условий (1) и требования « должна быть выпуклой по Х и вогнутой по
должна быть выпуклой по Х и вогнутой по 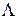 в окрестности
в окрестности  » для существования «седла».
» для существования «седла».
Поиск по сайту: