 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Симплекс-метод. Пример. Рассмотрим задачу оптимизации плана производства с целью получения максимальной прибыли (табл
Пример. Рассмотрим задачу оптимизации плана производства с целью получения максимальной прибыли (табл. 5).
Таблица 5
| Ресурсы | Норма расхода ресурсов | Запас ресурса | |||
| П1 | П2 | П3 | П4 | ||
| Трудовые | |||||
| Сырье | |||||
| Оборудование | |||||
| Прибыль | - | ||||
| План | х1 | х2 | х3 | х4 | - |
Решение. Математическая модель задачи:
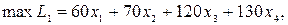
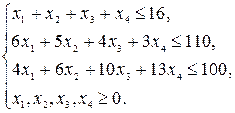
В ограничения задачи введем дополнительные переменные y1, y2, y3 перепишем условие задачи в виде уравнений:
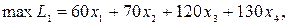
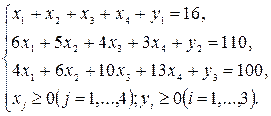
Эту подстановку можно переписать в виде рис. 6.

Рис. 6
Последнюю постановку можно представить в виде таблицы - первой таблицы симплекс-метода.
Правила составления симплекс-таблиц.
Для первой таблицы:
1) в первый столбец записывают уi - базисные переменные, которые находятся в уравнениях слева;
2) свободные переменные xi, заключенные в скобках, выносят в верхнюю строку таблицы;
3) в остальные столбцы записывают коэффициенты перед свободными переменными;
4) индексная строка есть результат вычитания из нуля коэффициентов перед свободными переменными.
Для последующих таблиц (табл. 6, 7, 8, 9):
1) выбирается наименьший отрицательный элемент в индексной строке при отыскании максимума, но наибольший положительный - при отыскании минимума, исключая вектор свободных членов;
2) этот элемент определяет ключевой вектор-столбец, и он вводится в базис;
3) компоненты вектора свободных членов делятся на положительные элементы ключевого столбца;
4) из полученных отношений выбирается наименьшее;
Таблица 6
Первая симплекс-таблица
| Базис | Свободные члены | Свободные переменные | |||
| х1 | х2 | х3 | х4 | ||
| y1 | |||||
| y2 | |||||
| y3 | |||||
| Индексная строка | -60 | -70 | -120 | -130 |
Таблица 7
Вторая симплекс-таблица
| Базис | Свободные члены | Свободные переменные | |||
| х1 | х2 | х3 | х4 | ||
| y1 | 108/13 | 9/13 | 7/13 | 3/13 | |
| y2 | 1130/13 | 66/13 | 47/13 | 22/13 | |
| x4 | 100/13 | 4/13 | 6/13 | 10/13 | |
| Индексная строка | -20 | -10 | -20 |
Таблица 8
Третья симплекс-таблица
| Базис | Свободные члены | Свободные переменные | |||
| х1 | х2 | х3 | х4 | ||
| x1 | 7/9 | 1/3 | |||
| y2 | -1/3 | ||||
| x4 | 2/9 | 26/39 | |||
| Индексная строка | 50/9 | -40/3 |
Таблица 9
Последняя симплекс-таблица
| Базис | Свободные члены | Свободные переменные | |||
| х1 | х2 | х3 | х4 | ||
| x1 | 1/18 | … | |||
| y2 | -1/3 | … | |||
| x4 | 13/6 | … | |||
| Индексная строка | 70/9 | … |
5) вектор-строка, содержащая наименьшее положительное частное, - ключевая и выводится из базиса;
6) на пересечении ключевых строк и столбца находится разрешающий элемент;
7) преобразование матрицы:
7.1. Каждый элемент ключевой строки делится на разрешающий элемент. Полученные частные являются элементами ключевой строки следующей таблицы.
7.2.Ключевой столбец в новой таблице - нули, за исключением разрешающего элемента.
Остальные элементы новой таблицы рассчитываются по схеме:
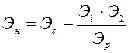
где Эн - новый элемент; Эс - старый элемент; Э1 - элемент ключевой строки; Э2 - элемент ключевого столбца; Эр - разрешающий элемент.
7.4. Если нулевая строка (столбец) содержит нуль, то соответствующий столбец (строка) в новой таблице не изменится.
Пункты 1-7 повторяются до тех пор, пока в индексной строке не останется ни одного- отрицательного элемента при отыскании максимума (но ни одного положительного при отыскании минимума).
Из последней таблицы видно, что:
1) в столбце свободных членов все элементы положительны, это значит, что полученное решение является допустимым;
2) в индексной строке все элементы также положительны. Это значит, что полученное решение - оптимально, т.е. максимизирует целевую функцию. При этом оптимальным планом будут величины: 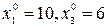 (значит, они базисные);
(значит, они базисные); 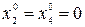 (так как они свободные), целевая функция L =1320.
(так как они свободные), целевая функция L =1320.
Из этой таблицы также следует, что базисная переменная у2= 26, а свободные переменные у1=у3= 0, т.е. в оптимальном плане резервы трудовых ресурсов и оборудования равны нулю, так как они используются полностью. А резерв ресурсов сырья у2= 26, что свидетельствует о его излишках.
Поиск по сайту: