 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД
Данный метод применяется, если система линейных ограничений – это система с базисом, но правые части равенств содержат отрицательные переменные. В отличие от симплекс-метода, первое, что делается – это выбор ведущей строки (ранее сперва выбирался столбец). Делается это так: в столбце  выбираем наименьший среди отрицательных.
выбираем наименьший среди отрицательных.
Далее выбираем ведущий столбец. Столбец с индексом  – ведущий, если:
– ведущий, если:

Замечание 1:
Таблица будет допустимой, если все элементы строки  неотрицательны.
неотрицательны.
Замечание 2:
Таблица будет оптимальной, если все элементы столбца  неотрицательны.
неотрицательны.
Условие неразрешимости задачи:
Если на некотором шаге окажется, что в столбце  есть отрицательный элемент, а среди элементов этой строки (в которую входит отрицательный элемент из столбца
есть отрицательный элемент, а среди элементов этой строки (в которую входит отрицательный элемент из столбца  ) нет отрицательных, то задача неразрешима.
) нет отрицательных, то задача неразрешима.
Пример:
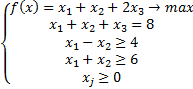
Важнейшее условие: система должна содержать базисные переменные. В первом уравнении у нас есть базисная переменная –  . При это уравнение является равенством. С другими двумя уравнениями нам повезло меньше.
. При это уравнение является равенством. С другими двумя уравнениями нам повезло меньше.
Преобразуем второе уравнение в равенство, для этого от левой части нужно что-то отнять. Добавляем  . Теперь, чтобы эта переменная преобразовалась в базинсую, у множим обе части этого уранвения на
. Теперь, чтобы эта переменная преобразовалась в базинсую, у множим обе части этого уранвения на  . Аналогично поступим с третьим уранвением.
. Аналогично поступим с третьим уранвением.

| Базисные перемен. | 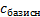
| 
| |||||

| 
| 
| 
| 
| |||



| -4 -6 | -1 | -1 | ||||

|
Ведущей строкой будет та, в которой отрицательный элемент столбца  наименьший – это строка
наименьший – это строка  с элементом -6. Ведущим столбцом будет
с элементом -6. Ведущим столбцом будет  .
.
| Базисные перемен. | 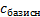
| 
| |||||

| 
| 
| 
| 
| |||



| -4 -6 | -1 | -1 | ||||

| |||||||



| -1 -1 | ||||||

|
Таблица сразу получилась оптимальной.
Получили оптимальный план:  .
.
| 24.11.2012 Практика |
Задача 1:

Базисная переменная только одна –  . Добавим переменные
. Добавим переменные  и
и  со знаком минус в левые части неравенств, чтобы получить из них равенства. Затем домножим два получившихся равенства на минус единицу, чтобы добавленные переменные входили в равенства с коэффициентами плюс один. В этом случае они становятся базисными.
со знаком минус в левые части неравенств, чтобы получить из них равенства. Затем домножим два получившихся равенства на минус единицу, чтобы добавленные переменные входили в равенства с коэффициентами плюс один. В этом случае они становятся базисными.

Видим, что в правой части двух последних неравенств у нас стоят отрицательные элементы. Это основание чтобы использовать двойственный симплекс-метод.
Составим таблицу, предварительно умножим целевую функцию на минус единицу, т. к. она у нас на  ,а для использования этого метода требуется задача нам
,а для использования этого метода требуется задача нам 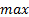 .
.
| Базисные перемен. | 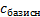
| 
| -2 | |||||

| 
| 
| 
| 
| 
| |||



| -18 -36 | -3 | -2 | -1 | ||||

| -1 | -1 |
По условию допустимости (задача является допустимой, если все элементы строки  отличны от нуля), задача является недопустимой, а значит, использовать метод двойственного симплекс-метода нельзя.
отличны от нуля), задача является недопустимой, а значит, использовать метод двойственного симплекс-метода нельзя.
Поэтому применим метод искусственного базиса.
| 01.12.2012 Лекция |
Задача 1.

Попробуем решить задачу двойственным методом.
Добавим в первые два уравнения по одной базисной переменной, при этом умножим на -1 там, где требуется для уравнивания знака неравенства и коэффициента при базисной. Получим систему:

| Базисные перемен. | 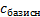
| 
| -3 | |||||

| 
| 
| 
| 
| 
| |||



| -10 | -1 | -4 -2 -2 | -1 | ||||

| -8 |
Оказалось, в строке  имеем отрицательный элемент, значит, двойственный метод не подходит, поэтому решаем методом искусственного базиса. Значит, второе уравнение мы не умножаем на -1, а добавляем в него переменную
имеем отрицательный элемент, значит, двойственный метод не подходит, поэтому решаем методом искусственного базиса. Значит, второе уравнение мы не умножаем на -1, а добавляем в него переменную 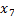 :
:

Добавляем столбец  , строку
, строку 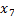 и строку
и строку  .
.
Во второй таблице переменная 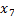 уйдёт из базиса из-за перестановки местами столбца
уйдёт из базиса из-за перестановки местами столбца  и строки
и строки 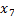 по ведущему элементу. Поэтому после второй таблицы столбик
по ведущему элементу. Поэтому после второй таблицы столбик  и строку
и строку 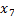 убираем.
убираем.
| Базисные перемен. | 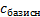
| 
| -3 | 
| |||||

| 
| 
| 
| 
| 
| 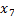
| |||

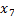

|

| -1 | -4 -2 -2 | -1 | |||||

| -8 | ||||||||

| -10 | -1 | -2 | ||||||



| 1/2 | -1/2 | -2 -1/2 -1 | ||||||

| -1 | ||||||||

|
Как видим, в строке  снова появился отрицательный элемент. Это означает, что задача неразрешима, т. е. не имеет оптимального решения.
снова появился отрицательный элемент. Это означает, что задача неразрешима, т. е. не имеет оптимального решения.
Задача 2.
Имеются стальные прутья длиной 110 сантиметров. Из них нужно нарезать заготовки длиной 45, 35 и 50 см. Определить, сколько прутьев и каким образом следует разрезать, что при минимальных отходах получить не менее 40, 30 и 20 заготовок соответственно.
Построим таблицу всевозможных вариантов разреза:
| 1 вариант | 2 вариант | 3 вариант | 4 вариант | 5 вариант | 6 вариант | |
| 45 см | - | - | - | |||
| 35 см | - | - | - | |||
| 50 см | - | - | - | |||
| Отходов |
Теперь нам нужно определить, сколько прутьев мы разрежем по каждому из способов, для удовлетворения условиям задачи.
Определим переменные:  – это количество прутьев, разрезанных по
– это количество прутьев, разрезанных по  му способу.
му способу.
Определим линейные ограничения: 
Составим задачу:

Решим двойственным методом – добавим базисные переменные в левую часть со знаком минус и домножим уравнения на -1. Замечаем, что целевая функция дана на минимум. Для решения задачи данным методом, нужно привести её к виду на максимум. Для этого умножим на -1 целевую функцию.

Составим таблицу.
Помним, что оптимальным решением будет то, при котором в столбце  не будет отрицательных элементов.
не будет отрицательных элементов.
| Базисные перемен. | 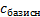
| 
| -20 | -15 | -5 | -25 | -10 | -30 | |||

| 
| 
| 
| 
| 
| 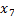
| 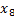
| 
| |||
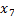
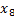

| -40 -30 -20 | -2 | -1 -2 | -3 | -1 -1 | -2 | -1 -1 | ||||

| |||||||||||

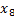

| -20 | -30 -20 | 1/2 -1 | -3 | -1 -1 | -2 | ½ -1 | -1/2 | |||

| -400 | ||||||||||



| -20 -5 | -20 | 1/2 -1 | 1/3 -1 | -2 | 1/2 1/3 | -1/2 | -1/3 | |||

| -450 | 70/3 | 55/3 | 5/3 | |||||||



| -20 -5 -10 | 1/2 1/2 | 1/2 1/2 | 1/2 1/3 | -1/2 | -1/3 | -1/2 | ||||

| -550 | 55/3 | 55/3 | 5/3 |
Наконец, получили неотрицательный столбец  . Ответ смотрим в столбце
. Ответ смотрим в столбце 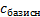 . оптимальный план – это 20 прутьев, изготовленных по первому способу, 5 прутьев – по третьему и ещё 10 – по пятому. При этом суммарные отходы составят 550 см.
. оптимальный план – это 20 прутьев, изготовленных по первому способу, 5 прутьев – по третьему и ещё 10 – по пятому. При этом суммарные отходы составят 550 см.
Поиск по сайту: