 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задание: решить геометрически.
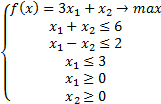
Построим область на координатной плоскости, зная, что  ,
,  . Для этого найдём точки, через которые проходит каждая из пяти прямых.
. Для этого найдём точки, через которые проходит каждая из пяти прямых.
Первая прямая 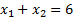 , очевидно, проходит через точки
, очевидно, проходит через точки  и
и 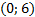 :
:  ,
, 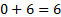 .
.
Вторая прямая 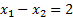 проходит через точки
проходит через точки  и
и 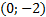 .
.
Остальные прямые совпадают с координатными осями.
Построим ограниченную данными прямыми область  :
:

По условию нужно найти наибольшее значение функции на данной области (значение 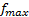 ). Функция принимает наибольшее значение в одной из точек пересечения целевой функции
). Функция принимает наибольшее значение в одной из точек пересечения целевой функции  и найденной области
и найденной области  . Чтобы найти эту точку, нам необходимо установить направление наискорейшего возрастания функции. Оно определяется вектором-градиентом:
. Чтобы найти эту точку, нам необходимо установить направление наискорейшего возрастания функции. Оно определяется вектором-градиентом:

По условию целевая функция имеет вид  . Найдём её первые частные производные:
. Найдём её первые частные производные:
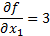
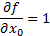
Таким образом, вектор-градиент направлен из начала координат в точку  .
.
Проведём перпендикуляр к градиенту и выполним его параллельный перенос в ту сторону, в которую направлен наш градиент. Переносим до тех пор, пока не встретим самую последнюю в этом направлении точку области  . В этой точке функция будет принимать наибольшее значение. Как видно по графику, это точка пересечения прямых
. В этой точке функция будет принимать наибольшее значение. Как видно по графику, это точка пересечения прямых  и
и 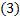 с координатами
с координатами  .
.
Подставим найденную точку в уравнение целевой функции, чтобы найти максимальное значение функции в данной области:
 .
.
| 13.09.2012 Лекция |
Запишем задачу линейного программирования в векторной форме. Вспомним вид обычной записи задачи линейного программирования:
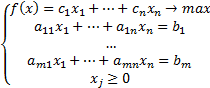
Видим, что правая часть целевой функции напоминает скалярное произведение векторов. Таким образом, целевая функция представима в виде скалярного произведения векторов  и
и  :
:

Ограничения же – это уравнения, которые в векторной форме можно представить так:

где
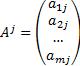 для любых
для любых 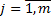


План  из
из 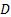 называется опорным, базисным, если он либо нулевой вектор, либо если система вектор-столбцов, соответствующих ненулевым координатам вектора х, является линейно независимой.
называется опорным, базисным, если он либо нулевой вектор, либо если система вектор-столбцов, соответствующих ненулевым координатам вектора х, является линейно независимой.
Пример:
Является ли вектор  базисным (опорным)?
базисным (опорным)?
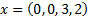
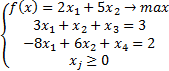
Но прежде чем проверять опорность плана  , следует сначала удостовериться, что
, следует сначала удостовериться, что  является планом, т. е. принадлежит множеству
является планом, т. е. принадлежит множеству 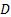 . Для этого подставим вектор
. Для этого подставим вектор  в ограничения:
в ограничения:
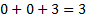
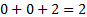
Следовательно, вектор  принадлежит множеству
принадлежит множеству 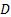 , т. е. является планом.
, т. е. является планом.
Теперь проверим, является ли план  базисным, для этого воспользуемся определением. Т. к. вектор
базисным, для этого воспользуемся определением. Т. к. вектор  не является нулевым, построим систему вектор-столбцов:
не является нулевым, построим систему вектор-столбцов:
Из вектора  только третья и четвёртая координаты является ненулевыми.
только третья и четвёртая координаты является ненулевыми.
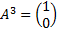

Установим наличие или отсутствие линейной зависимости этих двух векторов. Помним, что система векторов  является линейно зависимой, если существуют такие
является линейно зависимой, если существуют такие  , не все равные нулю, при которых
, не все равные нулю, при которых 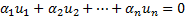 .
.
Следовательно, система векторов не является линейно зависимой. Таким образом, можем сделать заключение: план  является базисным (опорным).
является базисным (опорным).
Определение:
Точка  множетсва
множетсва 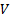 называется угловой точкой множества
называется угловой точкой множества 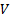 , если она не является внутренней точкой никакого отрезка.
, если она не является внутренней точкой никакого отрезка.
Определение:
Множество 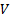 называется выпуклым, если оно вместе с любыми двумя точками содержит и весь отрезок, заключённый между этими точками.
называется выпуклым, если оно вместе с любыми двумя точками содержит и весь отрезок, заключённый между этими точками.
Запишем условие принадлежности отрезка всему множеству:
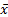 ,
, 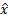
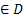

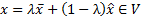 ,
, 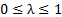
Теорема:
Каждый базисный план является угловой точкой множества допустимых планов.
Доказательство:
Существует некий  , являющийся планом, т. е.
, являющийся планом, т. е. 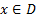 . Кроме того, по условию
. Кроме того, по условию  – базис. Докажем, что
– базис. Докажем, что  – угловая точка.
– угловая точка.
Поскольку  базисный, у него есть как нулевые, так и ненулевые координаты. Допустим,
базисный, у него есть как нулевые, так и ненулевые координаты. Допустим,  . Из этого следует, что система
. Из этого следует, что система 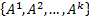 линейно независима.
линейно независима.
Докажем от противного, т. е. пусть  не является угловой точкой, другими словами,
не является угловой точкой, другими словами,  – внутренняя точка некоторого отрезка. Отсюда следует, что
– внутренняя точка некоторого отрезка. Отсюда следует, что  , где
, где 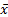 ,
, 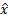
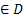 . Запишем это равенство в координатном виде:
. Запишем это равенство в координатном виде:
 ,
, 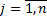 .
.
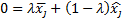 ,
, 
По условию задачи линейного программирования, координаты у допустимых планов неотрицательны, т. е.  и
и  .
.
Т. к.  , то в правой части последнего равенства стоит сумма неотрицательных слагаемых. Это происходит тогда, когда все члены равенства равны нулю, т. е.
, то в правой части последнего равенства стоит сумма неотрицательных слагаемых. Это происходит тогда, когда все члены равенства равны нулю, т. е. 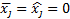 ,
,  . Т. е. у векторов
. Т. е. у векторов 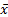 и
и 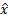
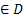 нулю равны одни и те же координаты.
нулю равны одни и те же координаты.
Т. к. 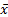 ,
, 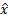
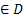 , они удовлетвряют ограничениям задачи:
, они удовлетвряют ограничениям задачи: 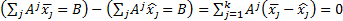 . Для
. Для 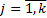
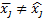 . Т. е. система вектор-столбцов
. Т. е. система вектор-столбцов 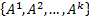 – линейно зависима <дописать здесь>.
– линейно зависима <дописать здесь>.
Теорема:
Если целевая функция принимает наибольшее значение в некоторой точке множества D, то она принимает это же значение и в некоторой угловой точке этого множества.
Доказательство:
Воспользуемся известным фактом: если D замкнутое, имеющее конечное число угловых точек (скажем, D – это какой-либо многоугольник), то любую точку из D можно представить в виде линейной комбинации угловых точек, т. е. если векторы  – угловые точки множества D, то для любых
– угловые точки множества D, то для любых 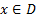 верно следующее:
верно следующее:

где 
Т. е. любая точка множества представима в виде угловой точки.
Пусть для любых 
 принимает наибольшее значение в точке
принимает наибольшее значение в точке  (скалярное произведение линейно по каждому сомножителю)
(скалярное произведение линейно по каждому сомножителю) 
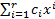 .
.
Выберем среди угловых точек  такую, в которой целевая функция принимает наибольшее значение. Такую точку выбрать возможно, ведь у нас конечное множество угловых точек. Среди угловых точек выберем такую, значение которой в целевой функции является наибольшим.
такую, в которой целевая функция принимает наибольшее значение. Такую точку выбрать возможно, ведь у нас конечное множество угловых точек. Среди угловых точек выберем такую, значение которой в целевой функции является наибольшим.
<дописать здесь>

 .
.
Итак,  .
.
Но с другой стороны,  :
: 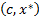 – наибольшее, т. е. для любого
– наибольшее, т. е. для любого 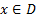 из
из 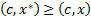 следует
следует 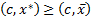 .
.
Из этого следует, что  . Что и требовалось доказать.
. Что и требовалось доказать.
Задача 1.

Решить нужно графически.
Построим область, ограниченную нашими прямыми и осями координат:
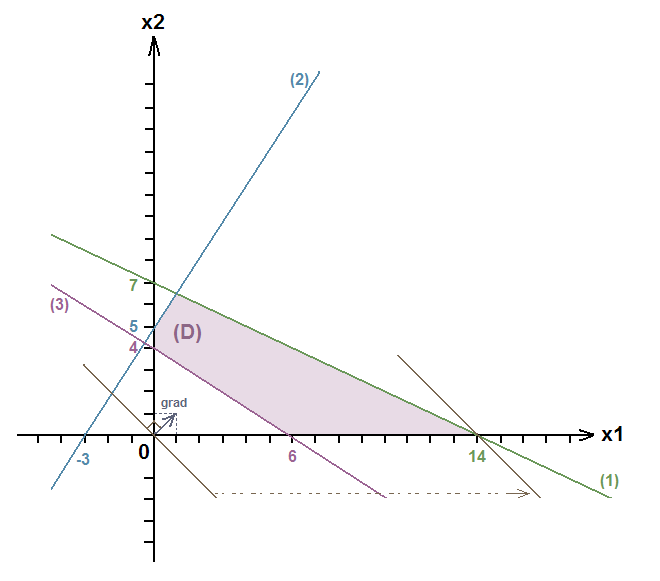
Найдём координаты вектора-градиента:

Прямую, перпендикулярную вектору-градиенту, параллельно переносим до пересечения с самой последней точкой, у нас это точка пересечения прямой 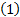 с осью координат
с осью координат  . Составим и решим систему:
. Составим и решим систему:
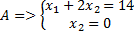
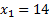 ,
, 

 – это и есть точка, в которой целевая функция принимает наибольшее значение.
– это и есть точка, в которой целевая функция принимает наибольшее значение.
Найдём значение целевой функции в этой точке:


 .
.
Задача 2.
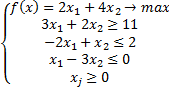
Построим область

Как видно на графике, область 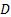 не ограничена. Следовательно, наибольшего значения у функции нет, задача решения не имеет. Целевая функция не ограничена сверху на непустом множестве планов.
не ограничена. Следовательно, наибольшего значения у функции нет, задача решения не имеет. Целевая функция не ограничена сверху на непустом множестве планов.
| 14.09.2012 Лекция |
Задача 3.
Продолжаем решать графически:
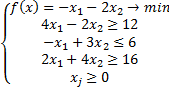

Вектор-градиент откладывается из начала координат в точку, координаты которой составлены из коэффициентов при целевой функции. Например, координатами вектора-градиента в этой задаче будут (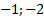 ), а направлен вектор-градиент всегда из начала координат.
), а направлен вектор-градиент всегда из начала координат.
Как мы помним, градиент показывает направление возрастания функции. Поэтому в задачах со стремящейся к минимуму целевой функцией мы переносим перпендикуляр градиента в ту сторону, которая противоположна его направлению. В этой задаче перпендикуляр градиента параллелен 3-ей прямой, а значит, при параллельном переносе он полностью накладывается на эту прямую. Это можно увидеть также по коэффициентам при аргументах целевой функции и третьего уравнения – они пропорциональны. Ответом к задаче будет множество точек, расположенных на том отрезке прямой 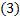 , который сходит в область
, который сходит в область 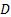 . Другими словами, это будут точки, расположенные на отрезке
. Другими словами, это будут точки, расположенные на отрезке  с координатами концов (
с координатами концов ( ) и (
) и (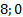 ).
).
Наш 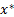 будет записан в виде:
будет записан в виде:  .
.
Подставим координаты концов отрезка 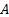 и
и  в целевую функцию:
в целевую функцию:

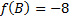
Таким образом, наименьшее значение целевой функции:  .
.
Задача 4.

<При желании решить эту задачу дома>
Задача 5.

Замечаем, что у нас больше двух переменных. Нам нужно выразить их все через  и
и  . Тогда целевая функция примет вот такой вид:
. Тогда целевая функция примет вот такой вид:

Упростим:
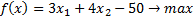
Теперь замечаем, что у нас нет неравенств. Без неравенств нам не удастся построить область. Чтобы получить неравенство из равенства, нужно одну из его частей увеличить или уменьшить. Видим, что наши 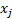 – неотрицательные, поэтому достаточно будет убрать из первой части уравнения любой
– неотрицательные, поэтому достаточно будет убрать из первой части уравнения любой  , чтобы точно получилось неравенство.
, чтобы точно получилось неравенство.
Уберём из левой части весь последний столбец  ’ов:
’ов:
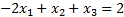



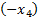




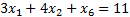
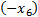

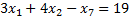

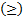
Таким образом, мы не только создали неравенства, но и избавились от столбца лишних переменных, и теперь сможем построить область.
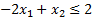
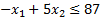

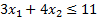

Находим:

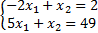

| 19.09.2012 Лекция |
Поиск по сайту: