 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПРАВИЛА ПЕРЕСЧЁТА СИМПЛЕКС-ТАБЛИЦЫ
Первое правило.
Столбец с индексом  объявляем ведущим, если
объявляем ведущим, если  , и над ним есть положительные элементы.
, и над ним есть положительные элементы.
Посмотрим на нашу таблицу выше. Если есть отрицательный элемент  , а над ним – хотя бы один положительный, то этот столбец мы можем выбрать ведущим.
, а над ним – хотя бы один положительный, то этот столбец мы можем выбрать ведущим.
Второе правило.
Строку с индексом  объявляем ведущей, если:
объявляем ведущей, если:

Делим  только на ненулевые и неотрицательные
только на ненулевые и неотрицательные  .
.
Третье правило.
Элемент  является ведущим. Это элемент, которых находится на пересечении выбранных ведущих строки и столбца.
является ведущим. Это элемент, которых находится на пересечении выбранных ведущих строки и столбца.
После того, как мы выбрали ведущую строку, ведущий столбец и сам ведущий элемент, начинаются правила непосредственно преобразования.
Четвёртое правило.
Ведущий элемент заменяется обратным. Т. е. выбранный элемент будет заменён на обратный ему.
Пятое правило.
Все элементы ведущей строки делим на ведущий элемент.
Шестое правило.
Все элементы ведущего столбца делим на минус ведущий элемент, т. е. столбец делится на противоположный по знаку ведущий элемент.
Седьмое правило.
Остальные элементы симплекс-таблицы вычисляются по формуле:

Восьмое правило.
Каждую симплекс-таблицу необходимо проверять на оптимальность и неразрешимость. Для этого введём следующее определение и теоремы.
Определение:
Симплекс-таблица называется допустимой, если элементы столбца  (за исключением, может быть, элемента
(за исключением, может быть, элемента  ) неотрицательны.
) неотрицательны.
Теорема (условие неограниченности целевой функции):
Если существует такой  , при котором
, при котором  , и над ним нет положительных элементов, то целевая функция
, и над ним нет положительных элементов, то целевая функция  не ограничена сверху на непустом множестве планов
не ограничена сверху на непустом множестве планов  .
.
Доказательство:
Рассмотрим вектор  при
при  . Докажем, что
. Докажем, что  . Для этого подставим
. Для этого подставим  в ограничения задачи.
в ограничения задачи.
Подставим для примера в нашу каноническую задачу, описанную в начале лекции. Подставим в первое ограничение:  – т. е. получили то же самое, что и у нас в первом ограничении. Следовательно, вектор
– т. е. получили то же самое, что и у нас в первом ограничении. Следовательно, вектор  .
.
Подставим вектор  в целевую функцию:
в целевую функцию:
 . По условию
. По условию  , тогда
, тогда  . Т. е. значение целевой функции неограниченно возрастает на непустом множестве планов. Задача неразрешима.
. Т. е. значение целевой функции неограниченно возрастает на непустом множестве планов. Задача неразрешима.
Теорема (условие оптимальности):
Если для любого 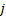 верно, что
верно, что 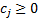 , то текущий опорный план оптимален.
, то текущий опорный план оптимален.
Доказательство:
По замечанию (2) в этой лекции значение целевой функции  на текущем опорном плане равно
на текущем опорном плане равно  . Рассмотрим произвольный
. Рассмотрим произвольный 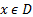 .
.
 . Все
. Все  по условию задачи, а все
по условию задачи, а все  по условию теоремы. Другими словами, для любого
по условию теоремы. Другими словами, для любого 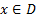
 . Отсюда вывод, что текущий опорный план оптимален.
. Отсюда вывод, что текущий опорный план оптимален.
Лемма (о ключевом отношении):
Если из базиса выводится переменная  , а в базис вводится переменная
, а в базис вводится переменная  , то следующая таблица будет допустимой.
, то следующая таблица будет допустимой.
Доказательство:
1.  . По пятому правилу пересчёта симплекс-таблицы мы
. По пятому правилу пересчёта симплекс-таблицы мы  делим на
делим на  . Элемент
. Элемент  , т. к. предыдущая симплекс-таблица была допустима. Элемент
, т. к. предыдущая симплекс-таблица была допустима. Элемент  у нас ведущий, а он по правилам пересчёта всегда больше нуля. Следовательно:
у нас ведущий, а он по правилам пересчёта всегда больше нуля. Следовательно:

2. По седьмому правилу пересчёта симплекс-таблицы, если  :
:

| 26.09.2012 Лекция |
Иными словами, если  , тогда
, тогда  , т. е.
, т. е. 
 симплекс-таблица допустима.
симплекс-таблица допустима.
3. Когда  . По правилу выбора ведущей строки имеем:
. По правилу выбора ведущей строки имеем:


Следовательно,


Задача:
Имеется три вида ресурсов, которые идут на производство трёх видов продукции.
| Ресурсы | Норма расхода ресурсов на производство единицы товаров 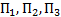
| Запас ресурсов | ||
| 
| 
| ||

| ||||

| ||||

| ||||
| Доход от продажи единицы товара |
Определить объём выпуска продукции каждого вида, чтобы доход был максимальным. Переменными будет количество единиц продукции того или иного вида –  ,
,  ,
,  . Введём ограничения по ресурсам – нельзя израсходовать на производство продукта больше единиц ресурса, чем есть в запасе. Т. к. на производство единицы продукта
. Введём ограничения по ресурсам – нельзя израсходовать на производство продукта больше единиц ресурса, чем есть в запасе. Т. к. на производство единицы продукта 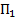 уходит 2 единицы ресурса
уходит 2 единицы ресурса  , на производство
, на производство 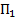 – 2 единицы ресурса
– 2 единицы ресурса  ,
,  – 4 единицы
– 4 единицы  . Тогда ограничение по ресурсу
. Тогда ограничение по ресурсу  будет выглядеть так:
будет выглядеть так:

Остальные ограничения:

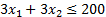
Целевая функция, исходя из условия максимизации дохода, будет выглядеть так:

Таким образом, получаем задачу:
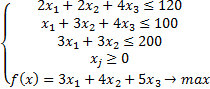
Помним, что уравнения в задаче должны быть базисными, т. е. в каждом уравнении должны быть переменные, которые входят только в одно уравнение, и только с коэффициентами 1. В симплекс-методе можно использовать только равенства, поэтому добавим в каждое уравнение переменные  ,
,  и
и  , чтобы неравенства превратить в равенства:
, чтобы неравенства превратить в равенства:

Каждая переменная  ,
,  и
и  входит с коэффициентом 1 и только в одно уравнение, следовательно, они стали нашими базисными переменными. Теперь, когда задача приведена к требуемому вид, можем составить симплекс-таблицу:
входит с коэффициентом 1 и только в одно уравнение, следовательно, они стали нашими базисными переменными. Теперь, когда задача приведена к требуемому вид, можем составить симплекс-таблицу:

| 
| 
| 
| |

| ||||

| ||||

| ||||

| -3 | -4 | -5 |
Выполним пересчёт симплекс-таблицы. Сперва выберем ведущий столбец. Ведущим может стать тот столбец, который содержит отрицательный элемент в строке  . У нас таких столбцов два –
. У нас таких столбцов два –  и
и  . Пусть это будет столбец
. Пусть это будет столбец  . Ведущая строка у нас будет выбрана по правилу
. Ведущая строка у нас будет выбрана по правилу  . Это строка
. Это строка  . Ведущий элемент находится на пересечении ведущего столбца и ведущей строки – это 2.
. Ведущий элемент находится на пересечении ведущего столбца и ведущей строки – это 2.
Меняем элемент в шапке  местами с элементом
местами с элементом  , ведущий элемент 2 заменяем на обратный. Затем каждый элемент ведущей строки делим на обратный ведущий элемент, а каждый элемент ведущего столбца – на обратный ведущий элемент со знаком минус (на -1/2). Остальные элементы пересчитываем по правилу прямоугольника: строим прямоугольник, противоположные элементы перемножаем, делим результат на неперевёрнутый ведущий элемент, и получившееся вычитаем из текущего значения элемента, который мы пересчитываем. Например:
, ведущий элемент 2 заменяем на обратный. Затем каждый элемент ведущей строки делим на обратный ведущий элемент, а каждый элемент ведущего столбца – на обратный ведущий элемент со знаком минус (на -1/2). Остальные элементы пересчитываем по правилу прямоугольника: строим прямоугольник, противоположные элементы перемножаем, делим результат на неперевёрнутый ведущий элемент, и получившееся вычитаем из текущего значения элемента, который мы пересчитываем. Например:
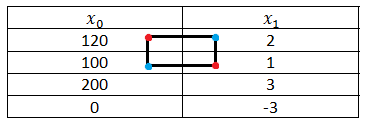

Результат пересчёта записываем в таблицу:

| 
| 
| 
| |

| 1/2 | |||

| -1/2 | |||

| -3/2 | -6 | ||

| 3/2 | -1 |
Теперь проверим задачу на оптимальность и разрешимость. Мы должны были сделать это в самом начале, но никогда не поздно. В самой нижней строке (элементы  ,
,  и
и  ) есть неотрицательные элементы, следовательно, таблица не является оптимальной. Таблица не является ни оптимальной, ни разрешимой.
) есть неотрицательные элементы, следовательно, таблица не является оптимальной. Таблица не является ни оптимальной, ни разрешимой.
Теперь заново пересчитываем всю таблицу. Выбираем ведущий столбец. Выберем тот элемент, при котором в строке  стоит отрицательный элемент – это столбец
стоит отрицательный элемент – это столбец  . Ведущая строка выбирается по правилу
. Ведущая строка выбирается по правилу  , это строка
, это строка  . Ведущий элемент – 2.
. Ведущий элемент – 2.

| 
| 
| 
| |

| 3/4 | -1/2 | ||

| -1/4 | 1/2 | ||

| -3/2 | -6 | ||

| 5/4 | 1/2 |
Некоторые из пересчитанных элементов (для примера):

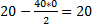


И т. д.
Получили в нашей таблице следующие значения  :
:
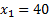

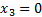
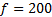
Следует запомнить следующее правило: из таблицы в таблицу значение  должно только увеличиваться.
должно только увеличиваться.
Проверим таблицу на оптимальность: в нижней строке (5/4, 1/2, 2) нет отрицательных элементов. Следовательно, таблица оптимальна.
Таким образом, получили ответ:  .
.
Задача решена.
Попробуем решить эту задачу другим способом. Он легче и удобнее, потому что в нём не используется пересчёт прямоугольником. Поменяем исходные данные:
| Ресурсы | Норма расхода ресурсов на производство единицы товаров 
| Запас ресурсов | ||
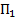
| 
| 
| ||

| ||||

| ||||

| ||||
| Доход от продажи единицы товара |

Также приведём уравнения к равенству:

| Базисные перемен. | 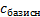
| 
| ||||||

| 
| 
| 
| 
| 
| |||



| ||||||||

| -9 | -10 | -16 | |||||



| 3/4 11/4 | 1/2 3/2 | -3/2 1/8 -3/8 | |||||

| -2 | |||||||
| 1/9 | -1/6 | |||||||
| 2/9 | 5/3 |
Эта таблица хороша тем, что целевая функция не обязательно должна быть выражена через базисные элементы. 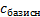 – это коэффициенты перед базисными переменными в целевой функции.
– это коэффициенты перед базисными переменными в целевой функции.
Строка  здесь – это скалярное произведение:
здесь – это скалярное произведение:
· Для клетки  –
– 
· Для остальных клеток –  минус верхние коэффициенты.
минус верхние коэффициенты.
Теперь выберем ведущий столбец. Среди отрицательных элементов выберем наименьший – это -16. Тогда столбец будет  . Почему мы выбрали именно этот? Ну. Хотя бы потому что от реализации товара
. Почему мы выбрали именно этот? Ну. Хотя бы потому что от реализации товара  мы получаем наибольший доход. Это вполне естественная реакция – когда ничего неизвестно, выбираем то, что выгоднее. Ведущая строка –
мы получаем наибольший доход. Это вполне естественная реакция – когда ничего неизвестно, выбираем то, что выгоднее. Ведущая строка –  , т. к. это минимум среди отношений элементов столбца
, т. к. это минимум среди отношений элементов столбца
 и ведущего столбца. Получили ведущий элемент – 8.
и ведущего столбца. Получили ведущий элемент – 8.
Преобразование симплекс-таблицы – это гауссовы преобразования матрицы. На месте ведущего элемента будем получать единицу, а остальные элементы ведущего столбца – занулять.
Мы должны занулить элементы ведущего столбца. Работая с каждым элементом по-отдельности, умножаем элементы любой другой строки на такое число, чтобы при сложении результата с выделенным элементом на его месте получить 0. Например, для зануления нашего элемента 12 работаем с ведущей строкой. Умножаем элемент 8 на -3/2 и прибавляем к первой строке. Аналогично поступаем и с остальными элементами этой строки и складываем со строкой, в которой находится элемент 12
Таблица является оптимальной, если в строке  все элементы неотрицательны. Задача является неразрешимой, если в столбце над отрицательным элементом в строке
все элементы неотрицательны. Задача является неразрешимой, если в столбце над отрицательным элементом в строке  есть отрицательные элементы.
есть отрицательные элементы.
Выполним ещё одну итерацию. Ведущим столбцом будет  , ведущая строка –
, ведущая строка –  . Занулим элемент 9, затем посчитаем строку
. Занулим элемент 9, затем посчитаем строку  чтобы проверить, не является ли таблица оптимальной. Строка
чтобы проверить, не является ли таблица оптимальной. Строка  не содержит неотрицательных элементов, следовательно, симплекс-таблица оптимальна. Остальные элементы пересчитывать не будем, запишем только элементы столбца
не содержит неотрицательных элементов, следовательно, симплекс-таблица оптимальна. Остальные элементы пересчитывать не будем, запишем только элементы столбца  для записи ответа.
для записи ответа.
 ,
,  ,
, 
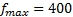 .
.
| 10.10.2012 Лекция |
В таблице некоторые элементы имеют экономический смысл. Например, элемент 1/2 в строке  столбца
столбца  означает, насколько надо уменьшить выпуск изделий третьего вида (
означает, насколько надо уменьшить выпуск изделий третьего вида ( ), чтобы ввести в план производства одно изделие второго вида (
), чтобы ввести в план производства одно изделие второго вида ( ). Т. е. мы не выпускаем половину изделия третьего вида, и на сэкономленные ресурсы можем выпустить одно изделие третьего вида.
). Т. е. мы не выпускаем половину изделия третьего вида, и на сэкономленные ресурсы можем выпустить одно изделие третьего вида.
Элементы 9 и 3/2 в столбце  показывают, сколько потребуется ресурса первого вида (
показывают, сколько потребуется ресурса первого вида ( ) и третьего вида (
) и третьего вида ( ) потребуется для введения в план производства одного изделия второго вида (
) потребуется для введения в план производства одного изделия второго вида ( ). При этом элемент -2 в строке
). При этом элемент -2 в строке  указывает, насколько увеличится доход. Он увеличится на 2.
указывает, насколько увеличится доход. Он увеличится на 2.
Элемент 96 в столбце  строки
строки  указывает на то, сколько единиц ресурса третьего вида остаётся неиспользованными при оптимальном плане производстве.
указывает на то, сколько единиц ресурса третьего вида остаётся неиспользованными при оптимальном плане производстве.
Другие элементы также имеют некоторую интерпретацию, которой коснёмся чуть позднее.
Поиск по сайту: