СИМПЛЕКС-МЕТОДЫ

Определение:

Система линейных уравнений называется системой с базисом, если в каждом уравнении есть уникальная переменная, т. е. переменная, которая содержится только в данном уравнении, причём с коэффициентом 1.

Определение:

Каноническая задача линейного программирования называется специальной, если:

1. система её ограничений – это система с базисом

2. целевая функция выражена только через небазисные переменные

3. правые части линейных ограничений неотрицательны, т. е. .

Внешний вид специальной задачи линейного программирования:

Проверим, является ли данная система специальной:

1. В каждом уравнении есть переменная, которая есть только в одном этом уравнении, причём с коэффициентом единица

2. выражена только через небазисные переменные

3. Все правые части неотрицательны.

Данная система действительно является специальной.

			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…
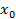
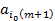
f			…		…

Замечание:

План является опорным.

Проверим, является ли планом. Подставим его координаты в линейные ограничения. Следовательно, 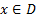. Теперь докажем, что план является опорным. Т. к. – ненулевой вектор, проверим, является ли система вектор-столбцов, соответствующих ненулевым координатам вектора , линейно независимой.

Первый вектор – – состоит из столбца коэффициентов при первой ненулевой координате – . Эти коэффициенты берём из нашей системы:

состоит из столбца коэффициентов при второй ненулевой координате – . И т. д.

Замечание:

Значение целевой функции на текущем опорном плане равно .

Докажем это. Текущий опорный план – это вектор . Подставим его в нашу целевую функцию: .

Теорема:

Множество опорных решений КЗЛП конечно.

Доказательство:

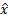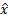Для доказательства конечности докажем, что различные планы имеют различную структуру. От противного: пусть , , , т. е. и 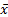– это два различных плана. Предположим, что они имеют одну и ту же структуру, т. е. нули стоят на одних и тех же местах.

Т. к. 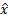, , они удовлетворяют системе ограничений.

_______________

Линейная комбинация равна нулю, т. е. векторы 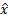, 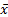линейно зависимы: существует такой 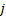, при котором 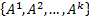– линейно зависимая система, что противоречит тому, что 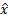, 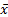– опорные планы.

Таким образом, разные планы имеют разную структуру, из чего следует, что нули различным образом на местах можно расставить конечное число раз. Отсюда следует, что множество опорных решений конечно. Теорема доказана.

Поиск по сайту: