 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
Имеем две задачи:
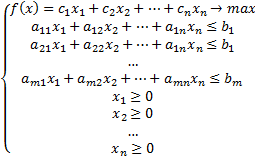
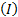 СЗЛП СЗЛП
| 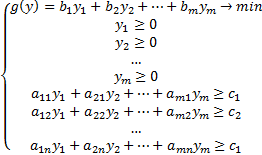
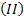
|
Системы 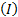 и
и 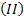 – пара симметрических двойственных задач. Из одной задачи всегда можно получить другую задачу.
– пара симметрических двойственных задач. Из одной задачи всегда можно получить другую задачу.
Правила построения двойственной задачи:
1. Необходимо согласовать знаки целевой функции и линейных ограничений:
· 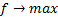 соответствует
соответствует 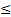
·  соответствует
соответствует 
· Если это не так, то помножаем на -1 либо  , либо ограничения
, либо ограничения
2. Каждому линейному неравенству ставится в соответствие неотрицательная переменная. В нашем примере у нас было 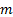 неравенств, в соответствии которым мы получили
неравенств, в соответствии которым мы получили 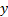 ’ки
’ки
3. Каждому уравнению ставится в соответствие переменная без ограничения в знаке (произвольная)
4. Каждой неотрицательной переменной ставится в соответствие неравенство
5. Каждой переменной без ограничения в знаке ставится в соответствие уравнение
Основное неравенство двойственности:
Для любого 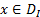 и любого
и любого 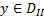 справедливо
справедливо 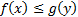 .
.
Доказательство:
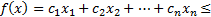

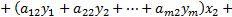


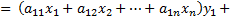


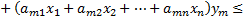
 , ч. т. д.
, ч. т. д.
Достаточно условие оптимальности:
Для любых планов 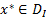 и
и 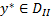 таких, что
таких, что 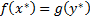 , то планы
, то планы 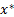 и
и 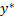 оптимальны в своих задачах.
оптимальны в своих задачах.
Первая теорема двойственности:
Если одна из пары двойственных задач разрешима, что разрешима и друга, причём 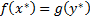 .
.
Доказательство:
Пусть задача 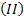 разрешима. Построим эквивалентную ей задачу
разрешима. Построим эквивалентную ей задачу  :
: 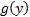 и все неравенства умножим на -1. Т. е. вся левая часть умножается на -1, и вместо
и все неравенства умножим на -1. Т. е. вся левая часть умножается на -1, и вместо  будет
будет 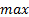 , а у неравенств знаки изменятся на противоположные. Таким образом, задача
, а у неравенств знаки изменятся на противоположные. Таким образом, задача 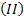 стала стандартной. Т. е. задача
стала стандартной. Т. е. задача  разрешима. Значит, разрешима двойственная к ней. Двойственная к задаче
разрешима. Значит, разрешима двойственная к ней. Двойственная к задаче  эквивалентна
эквивалентна 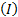 , т. е. задача
, т. е. задача 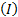 разрешима.
разрешима.
Определение:
Говорят, что планы 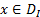 и
и 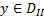 удовлетворяют условиям дополняющей нежёсткости (УДН), если в каждой паре сопряжённых неравенств одно обязательно выполняется как равенство.
удовлетворяют условиям дополняющей нежёсткости (УДН), если в каждой паре сопряжённых неравенств одно обязательно выполняется как равенство.
На данном определении основана вторая теорема двойственности:
Планы 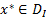 и
и 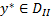 оптимальны тогда и только тогда, когда удовлетворяют условиям дополняющей нежёскости.
оптимальны тогда и только тогда, когда удовлетворяют условиям дополняющей нежёскости.
Доказательство:
В одну сторону: докажем, что выполняются УДН. Пусть планы 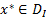 и
и 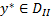 – оптимальны. Тогда по первой теореме двойственности
– оптимальны. Тогда по первой теореме двойственности 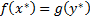 . Раз так, то неравенство
. Раз так, то неравенство 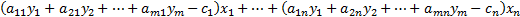 становится равно 0:
становится равно 0: 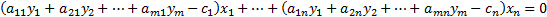 .
.
В левой части данного равенства записана сумма неотрицательных слагаемых, которая равна нулю только в случае равенства нулю каждого слагаемого.
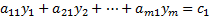 или
или 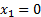

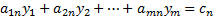 или
или 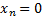
Т. е.  и
и 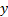 удовлетворяют условиям дополняющей надёжности.
удовлетворяют условиям дополняющей надёжности.
| 12.10.2012 Лекция |
Продолжим рассмотрение двойственных задач.
Вернёмся к задаче, которую решали первым способом:
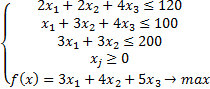
Мы уже нашли оптимальное решение этой задачи:
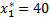
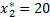

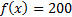
Строим двойственную к ней задачу:
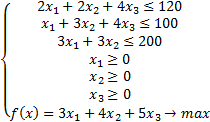
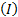
| 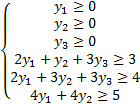
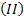
|
Подставим оптимальное решение задачи 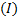 в ограничение задачи:
в ограничение задачи:
Если ограничение выполняется как равенство, то сопряжённое – как неравенство, и наоборот.
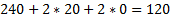
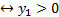 (по условию УДН)
(по условию УДН)
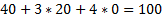
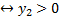
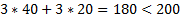
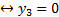
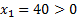
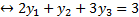
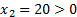
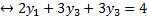
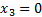
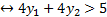
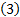
Выберем из получившихся сопряжённых равенства, получим:
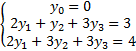

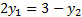
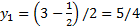
Получили ответ: 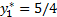 ,
, 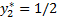 ,
,  ,
, 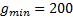 .
.
Таким образом мы продемонстрировали метод решения двойственной задачи. Вернёмся к эконмическому смыслу задачи. Правые части ограничений 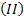 – 3, 4, 5 – выражены в денежных единицах. Тогда и левые – также в денежных единицах. Коэффициенты при переменных
– 3, 4, 5 – выражены в денежных единицах. Тогда и левые – также в денежных единицах. Коэффициенты при переменных 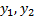 и
и 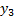 в ограничениях – это нормы затрат ресурсов каждого вида на единицу продукции одного вида. Поэтому
в ограничениях – это нормы затрат ресурсов каждого вида на единицу продукции одного вида. Поэтому 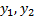 и
и 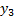 – это цены ресурсов. Значит, ответ задачи – это план оптимальных цен ресурсов.
– это цены ресурсов. Значит, ответ задачи – это план оптимальных цен ресурсов.
Правые части ограничений 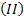 – это доход от реализации продукции конкретного вида, а левые части – это затраты на её производство. В
– это доход от реализации продукции конкретного вида, а левые части – это затраты на её производство. В 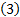 УДН свидетельствуют о том, что производится только так продукция (
УДН свидетельствуют о том, что производится только так продукция (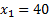 ,
,  ), для которой затраты равны доходу (видим равенства). Если затраты превышают доход (
), для которой затраты равны доходу (видим равенства). Если затраты превышают доход ( ), то такую продукцию производить невыгодно:
), то такую продукцию производить невыгодно: 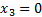 .
.
Коэффициенты при 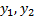 и
и 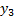 в целевой функции
в целевой функции 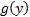 – это запасы ресурсов, а сами
– это запасы ресурсов, а сами 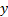 ’ки, как мы сказали, это цены ресурсов. Таким образом,
’ки, как мы сказали, это цены ресурсов. Таким образом, 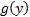 – это суммарные затраты на приобретение всех ресурсов.
– это суммарные затраты на приобретение всех ресурсов.
Задача 1.
Решим прямую задачу вторым способом записи симплекс-таблицы.
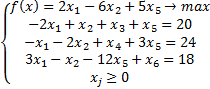
Целевая функция выражены как через базисные, так и через небазисные переменные, что значит, мы сможем решить её только вторым способом записи симплекс-таблицы. Помним, что базисные переменные – это те, которые входят только в одно уравнение и при том с коэффициентом 1. У нас это переменные  ,
,  ,
,  . В целевой функции этих переменных нет, поэтому в столбце
. В целевой функции этих переменных нет, поэтому в столбце 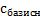 у нас нули.
у нас нули.
Выберем ведущий столбец. Им будет тот, в котором в строке  стоит отрицательный элемент. Выберем в данном столбце ведущую строку. Для этого элементы столбца
стоит отрицательный элемент. Выберем в данном столбце ведущую строку. Для этого элементы столбца  делим на элементы ведущего столбца, но помним о том, что делим только на неотрицательные элементы:
делим на элементы ведущего столбца, но помним о том, что делим только на неотрицательные элементы:
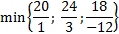
Отрицательный элемент -12 убираем, получаем
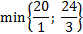

Тогда ведущий элемент будет в строке  столбца
столбца  .
.
Меняем местами базисную переменную  и элемент
и элемент  .
.
Теперь начинаем занулять элементы ведущего столбца с помощью обычных преобразований матриц, умножая строки на число и складывая их друг с другом. Нам нужно занулить все элементы кроме ведущего. Ведущий элемент должен принять значение 1. Например, для зануления элемента -12 умножим элементы строки  на 4 и сложим со строкой
на 4 и сложим со строкой  . Чтобы ведущий элемент принял значение 1, строку
. Чтобы ведущий элемент принял значение 1, строку  умножим на 1/3 и запишем результат в новой таблице. Чтобы занулить элемент 1, умножим элементы строки
умножим на 1/3 и запишем результат в новой таблице. Чтобы занулить элемент 1, умножим элементы строки  на -1/3 и сложим со строкой
на -1/3 и сложим со строкой  .
.
| Базисные перемен. | 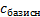
| 
| -6 | |||||

| 
| 
| 
| 
| 
| |||



| -2 -1 | -2 -1 | -12 | |||||

| -2 | -5 | ||||||



| -1 2/3 -1/3 -1 | 1 2/3 -2/5 -9 | 1/3 | -1/3 1/3 | ||||

| -3 2/3 | 2 2/3 | 5/8 |
Проверим таблицу на оптимальность и разрешимость. Столбец  не имеет неотрицательных элементов, и находится над отрицательным элементом в строке
не имеет неотрицательных элементов, и находится над отрицательным элементом в строке  , значит, задача не имеет решения.
, значит, задача не имеет решения.
Задача 2.
Решим прямую задачу вторым способом записи симплекс-таблицы.

| Базисные перемен. | 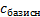
| 
| -1 | -1 | |||

| 
| 
| 
| 
| |||



| -1 -1 | ||||||

| -3 | ||||||



| -1 | ||||||
| 17.10.2012 Практика |
Задача 1:
Решить прямую и двойственную задачу
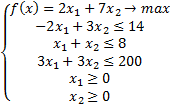
В нашей задаче только две переменные, поэтому решим графически:
Выразим  из первого уравнения:
из первого уравнения:
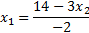
Из второго:
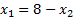
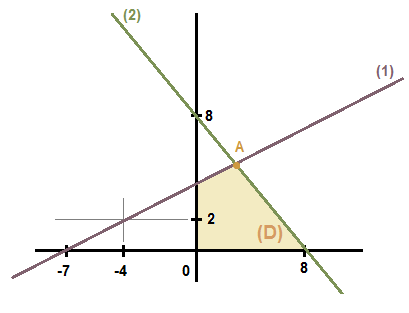
Найдём наибольшую точку области  :
:
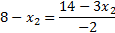
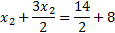

Наша точка:

Найдём значение целевой функции в этой точке:
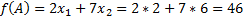
Составим двойственную к ней задачу:

Решим её:
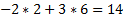

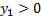
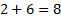

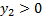
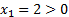

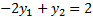
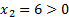

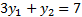
Решим как систему:

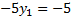
Нашли точку:


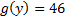
По теореме двойственности целевая функция в этой задаче имеет то же значение, что и у прямой задачи.
| 07.11.2012 Практика + самостоятельная в конце пары |
Решить задачу:
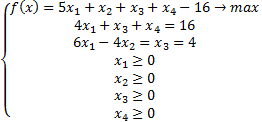
Чтобы решить задачу вторым симплекс-методом, нам требуются базисные переменные. Их у нас нет. Добавить их нельзя – в уравнениях стоят уже равенства. Поэтому решить задачу известными симплекс-методами нельзя. Тогда составим двойственную задачу, и на основании её решения решим прямую задачу.
Составим двойственную задачу:
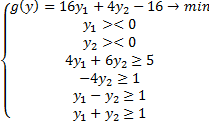
Теперь, когда задача составлена, её легко решить графически. Т. к.  и
и  имеют произвольный знак по отношению к 0, координатные оси не задают ограничений, т. е. мы строим нашу область на всей плоскости.
имеют произвольный знак по отношению к 0, координатные оси не задают ограничений, т. е. мы строим нашу область на всей плоскости.
Найдём точки, через которые проходит прямая 
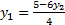
Точка минимума функции: 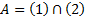
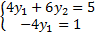
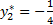
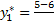
Решением будет найденное значение целевой функции в точке 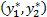 . Подставим эту точку в целевую функцию и найдём решение обратной задачи.
. Подставим эту точку в целевую функцию и найдём решение обратной задачи.
Теперь мы можем найти решение прямой задачи. Для этого, по второй теореме двойственности, нам необходимо доказать, что найденные планы удовлетворяют УДН, т. е. что в каждой паре сопряжённых неравенств одно обязательно выполняется как равенство. Сопряжённые неравенства – это соответствующие неравенства прямой задачи и обратной задачи. Подставим в условия обратной задачи найденные оптимальные планы:
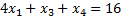

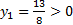
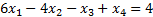

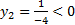
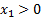

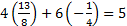
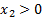

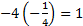
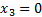


…
Задача 2:
Определить, является ли вектор  оптимальным решением следующей задачи:
оптимальным решением следующей задачи:
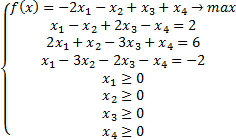
Предположим, что указанный план оптимален. Тогда по первой теореме двойственности значение целевой функции в этом плане будет совпадать со значением целевой функции в оптимальном плане обратной задачи. Однако нам неизвестен оптимальный план обратной задачи, его требуется найти.
Составим обратную задачу
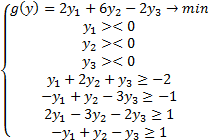
Теперь делаем примерно то же самое, что и в конце предыдущей задачи – подставляем план  в сопряжённые равенства. Т. к. план
в сопряжённые равенства. Т. к. план  принадлежит прямой задачи, в неё и подставляем:
принадлежит прямой задачи, в неё и подставляем:
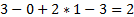

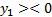
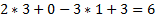


…
Теперь выделим из получившихся только равенства и решим их:
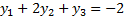

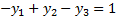
Сложим первое и третье:

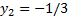
Теперь подставим в первое:
…
Самостоятельная работа.
Вариант 1.
| 13.11.2012 Лекция |
Поиск по сайту: