Задание 3. Решение задач линейного программирования симплекс-методом

Пример. Симплекс-методом решить ЗЛП:

(3.1)

при наличии ограничений:

(3.1)

, . (3.2)

Приводим систему линейных неравенств (3.1) к каноническому виду, вводя в каждое неравенство дополнительную переменную , 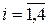. Получим систему линейных уравнений:

(3.3)

Целевая функция принимает вид

(3.4)

Расширенная матрица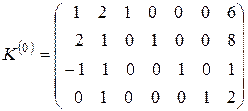

системы линейных уравнений (3.3) является исходной К -матрицей ЗЛП, которая определяет исходный опорный план:

, .

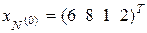Кроме того, .

Результаты последовательных итераций симплекс-алгоритма удобно оформить в виде симплекс-таблицы (см. табл. 3.1).

Таблица 3.1

S	i
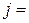
					-1						- -
		-3	-2					k =1 l =2
						3/2 1/2 3/2		-1/2 1/2 1/2			4/3 10/3
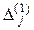
			-1/2		3/2			k =2 l =1
				4/3 10/3 2/3			2/3 -1/3 -1 -2/3	-1/3 2/3 1/3
				1/3	4/3

На второй итерации S = 2, все , следовательно, опорный план

, ,

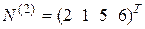определяемый К -матрицей К⁽²⁾, оптимальный. Тогда

, .

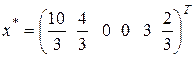Задания для самостоятельного выполнения

Предприятие производит 3 вида продукции: А₁, А₂, А₃, используя сырье двух видов: В₁ и В₂. Известны затраты сырья i -го вида на единицу изделия j -го вида (), количество сырья каждого вида (i =1,2), а так же прибыль, полученная от единицы изделия j -го вида с_j (j =1,2,3).

Сколько изделий каждого вида необходимо произвести, чтобы получить: 1) максимум прибыли;

2) максимум товарной продукции?

Обозначения для вариантов: в таблице приведена матрица затрат: А= (а_ij), справа от таблицы значение b_i (i =1,2) и внизу - с_j (j =1,2,3).

Поиск по сайту: