Задание 7. Решение задач линейного программирования на основе использования вычислителя OpenOffice Calc.org

Для решения задач оптимизации в MS Excel используют надстройку Поиск решения, которая вызывается из пункта главного меню «Сервис»(рис. 7.1).

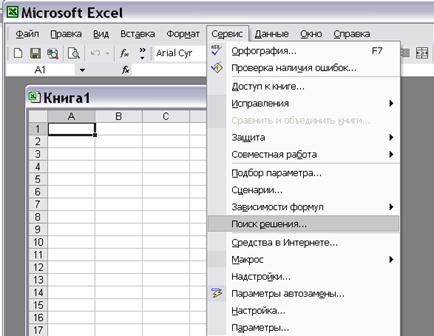
Рис. 7.1.

Если в версии Excel, установленной на Вашем компьютере, отсутствует данный подпункт меню «Сервис», необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения» (рис. 7.2).

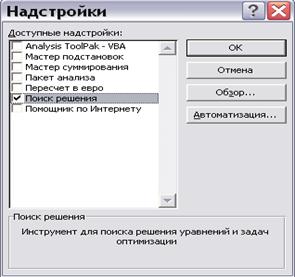
Рис. 7.2.

Рассмотрим на примере использование данной надстройки. Математическая модель задачи имеет вид:

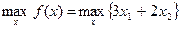
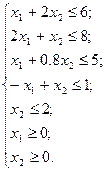
Составим шаблон в редакторе Excel, как показано на рис. 7.3.

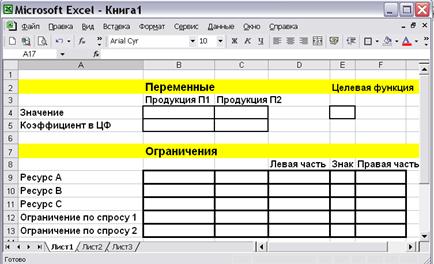
Рис. 7.3. Шаблон оформления задачи.

Теперь занесём данную в задаче числовую информацию (рис.7.4).

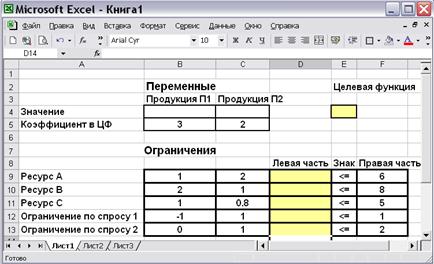
Рис.7.4. Исходные данные задачи

В выделенные пустые ячейки (значения целевой функции и левых частей неравенств) необходимо занести формулы, отображающие связи и отношения между числами на рабочем листе.

Ячейки B4 – С4 называются в Excel изменяемыми (в нашей модели это неизвестные переменные), т.е., изменяя их Поиск решения будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).

Теперь необходимо ввести формулы. В нашей математической модели, целевая функция представляет собой произведение вектора коэффициентов на вектор неизвестных. Действительно, выражение 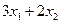можно рассматривать как произведение вектора (3,2) на вектор .

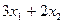В Excel существует функция СУММПРОИЗВ, которая позволяет найти скалярное произведение векторов. В ячейку Е4 необходимо вызвать данную функцию, а в качестве перемножаемых векторов задать адреса ячеек, содержащих коэффициенты уравнений (в данном случае, это В5:С5) и ячеек, в которые в результате решения будут помещены значения 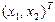(ячейки В4:С4) (рис. 7.5).

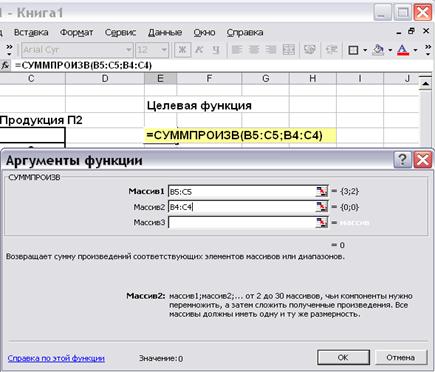
Рис. 7.5. Вызов функции СУММПРОИЗВ.

Каждая левая часть ограничения тоже представляет собой произведение двух векторов: соответствующей строки матрицы затрат и вектора неизвестных. То есть, выражение 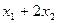(для первого ограничения ) будем рассматривать как произведение вектора коэффициентов (1,2) и вектора пока переменных .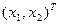

В ячейке, отведенной для формулы левой части первого ограничения (D9), вызовем функцию СУММПРОИЗВ. В качестве адресов перемножаемых векторов занесем адрес строки коэффициентов В9:С9 и адрес значений переменных В4:С4 (рис. 7.6).

Рис. 7.6

В четыре оставшиеся ячейки графы «Левая часть» вводим аналогичные формулы, используя соответствующую строку матрицы затрат. Фрагмент экрана с введёнными формулами показан на рис.7.7.

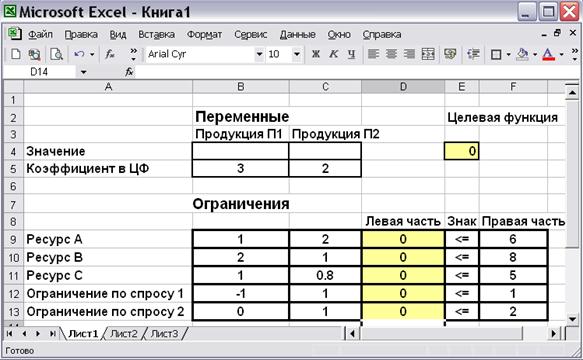
Рис. 7.7

Важно! К моменту вызова сервиса «Поиск решения» на рабочем листе с задачей должны быть занесены формулы для левых частей ограничений и формула для значения целевой функции.

В меню Сервис выбираем Поиск решения. В появившемся окне задаём следующую информацию:

1. в качестве целевой ячейки устанавливаем адрес ячейки для значения целевой функции Е4;

2. «флажок» устанавливаем на вариант «максимальному значению», т.к. в данном случае, целевая функция дохода подлежит максимизации;

3. в качестве изменяемых ячеек заносится адрес строки значений переменных В4:С4;

4. справа от окна, предназначенного для занесения ограничений, нажимаем кнопку «Добавить», появится форма для занесения ограничения (рис. 7.8)

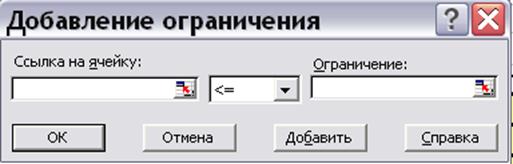
Рис.7.8. Форма для занесения одного ограничения ЗЛП.

5. в левой части формы «Ссылка на ячейку» заносится адрес формулы для левой части первого ограничения D9, выбирается требуемый знак неравенства (в нашем случае, <=), в поле «Ограничение» заносится ссылка на правую часть ограничения F9 (рис. 7.9).

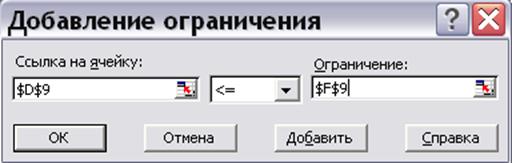
Рис.7.9. Занесение первого ограничения задачи.

Аналогично заносятся все ограничения задачи, после чего нажимается кнопка «ОК».

Таким образом, окно «Поиск решения» с занесенной информацией выглядит следующим образом (рис.7.10):

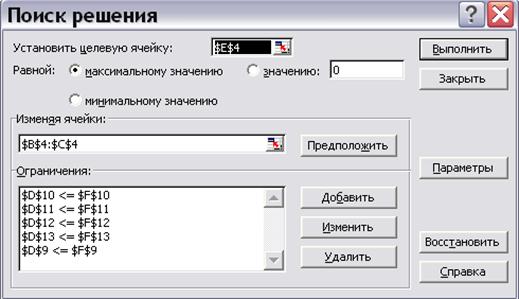
Рис. 7.10.

Далее необходимо нажать кнопку Параметры, установить «флажки» «Линейная модель» и «Неотрицательные значения», поскольку в данном случае задача является ЗЛП, а ограничение 6) требует неотрицательности значений (рис.7.11).

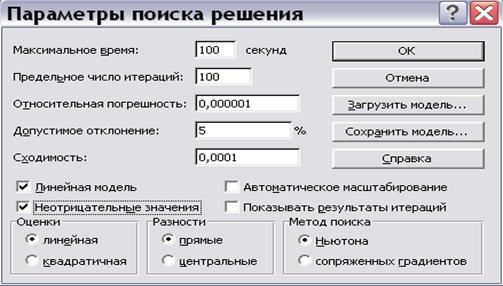
Рис. 7.11. Установка параметров

Затем следует нажать «ОК», «Выполнить», после чего появляется окно результата решения (рис.7.12).

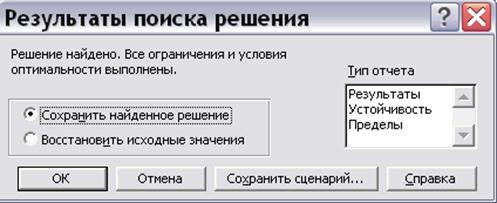
Рис. 7.12. Окно результата решения

Если в результате всех действий получено окно с сообщением «Решение найдено», то Вам предоставляется возможность получения трех типов отчета, которые полезны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав «ОК». В результате получено решение задачи (рис.7.13).

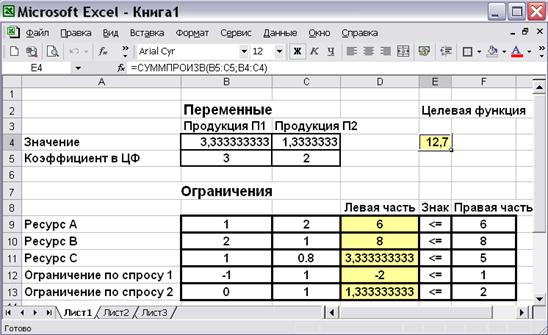
Рис.7.13. Результат применения «Поиска решения»

Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения (рис.7.14), это означает, что при оформлении задачи была допущена ошибка (не заполнены формулы для ограничений, неправильно установлен «флажок» максимизации/минимизации и т.д.).

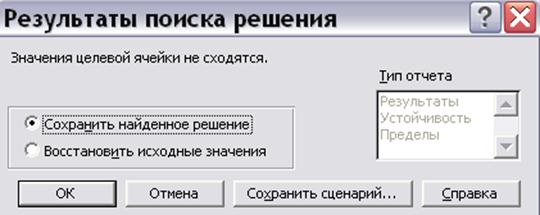
Рис.7.14. Сообщение об ошибке

В данном разделе рассмотрен общий формат решения задач оптимизации в Excel. В зависимости от экономических моделей, выполняют его соответствующие модификации.

Например, можно установить условие на целочисленность некоторых переменных.

Поиск по сайту: