Задание 6. Решение транспортных задач на основе метода потенциалов

Решить транспортную задачу:

Решение. Условие баланса выполнено. Следовательно, имеем ТЗ закрытого типа.

Предварительный этап. Находим исходный опорный план X° методом «минимального элемента».

Число занятых клеток равно 6 и совпадает с рангом матрицы ограничений ТЗ:

r = m + n - 1 = 3+4-1 = 6.

Итерация 1. Для проверки полученного опорного плана на оптимальность находим

систему потенциалов для занятых клеток (хij>0). Для этого, например, полагаем, что U1= 0 (записываем U1= 0 в левой вертикальной графе в табл. 2.2). Далее, исходя из занятых клеток (1, 2) и (1, 3), находим V2= С12-U1 = 4 - 0 = 4, V3 = 6 - 0 = 6 (записываем в верхней строке в таблице). На основе базисной клетки (2, 3) получаем U2=2 - 6 =-4, затем V1= 1-(-4) = 5; U3=3 - 4= -1; V4=2.

Далее вычисляем сумму потенциалов для каждой из свободных клеток и записываем их в верхнем левом углу. Так как для клеток (3,1) и (3,3) критерий оптимальности (условие B) не выполняется:

U3+ V1 = 4 > 2,

U3+ V3 = 5 > 3,

то полученный опорный план не оптимальный.

Так как Δ31= U3+ V1- Cij = 2 = Δ33, то в любую из клеток, например, в (3,1), ставим некоторое число θ1.

Для того чтобы не нарушился баланс в 3-ей строке, вычитаем θ1 из величины перевозки, стоящей в клетке (3, 2), прибавляем к Х12, вычитаем от Х13, прибавляем к Х23 и вычитаем от Х21, т.е. составляем цикл:

(3,1)->(3,2)->(1,2)->(1,3)->(2,3)->(2,1)->(3,1).

Знаки + и - в клетках чередуются.

Заметим, что движение от одной клетки к другой происходит только по занятым, кроме первой, в которую θ1 проставляется. Максимальное значение θ1 равно наименьшему уменьшаемому: θ1= 50. Если θ1 взять больше, то получаем отрицательную величину в плане перевозок, а если меньше, то нарушается опорность плана.

Итерация 2. Проверяем полученный план Х(1) на оптимальность. Находим систему потенциалов. Они записаны в таблице слева и сверху, вычисляем сумму потенциалов для свободных клеток (записаны в левом верхнем углу клетки). Так как U1+ V4 = 4 > 3, то план Х(1) не является оптимальным. Для построения нового опорного плана проставляем величину θ2 в клетку (1,4) и составляем цикл:

(1,4)->(3,4)>(3,1)->(2,1)->(2,3)->(1,3)->(1,4).

Определяем значение θ2 =50, при этом две клетки (1,3) и (3, 4) обращаются в нулевые. Следовательно, план Х(2) будет вырожденным. Для дальнейшего решения необходимо оставить нуль в одной из клеток и считать ее за базисную. Целесообразнее нуль оставить в клетке с меньшей стоимостью перевозок, т.е. в клетке (3,4).

Итерация 3. Число занятых клеток равно 6. Находим значения потенциалов и их сумму для свободных клеток. Критерий оптимальности выполняется:

Ui+ Vj≤ Cij для Хij= 0; i=1,m;j=1,n

поэтому полученный план является оптимальным: f (x)* = 1500

Решить транспортную задачу методом потенциалов:

1.

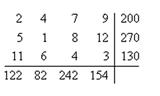
2.

3.

4.

5.

6.

7.

Поиск по сайту: