 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задание 5. Решение целочисленных задач линейного программирования на основе метода ветвей и границ
Рассмотрим задачу ЦЛП вида

 ,
,  ,
,
 ,
,  ,
,  ,
, 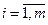 ,
,
 — целые,
— целые,  .
.
На первом шаге необходимо решить сформулированную задачу как задачу ЛП, рассматривая все ее переменные как непрерывные. Получаемая таким образом задача ЛП обозначается через ЛП-1, оптимальное значение ее целевой функции – через  . Пусть в оптимальном решении задачи ЛП-1 некоторые целочисленные переменные принимают дробные значения; тогда оптимальное решение исходной задачи не совпадает с оптимальным решением ЛП-1. В этом случае величина
. Пусть в оптимальном решении задачи ЛП-1 некоторые целочисленные переменные принимают дробные значения; тогда оптимальное решение исходной задачи не совпадает с оптимальным решением ЛП-1. В этом случае величина  представляет собой верхнюю границу оптимального значения исходной задачи.
представляет собой верхнюю границу оптимального значения исходной задачи.
На следующем шаге производится ветвление по одной из целочисленных переменных, имеющих дробное значение в оптимальном решении задачи ЛП-1. Часто выбирают переменную, которая имеет наибольшее дробное значение.
Пусть ветвление происходит по целочисленной переменной xj, значение которой в оптимальном решении ЛП-1 равно  . Далее рассматриваются две новые задачи ЛП, обозначаемые через ЛП-2 и ЛП-3. Они получаются путем введения ограничений
. Далее рассматриваются две новые задачи ЛП, обозначаемые через ЛП-2 и ЛП-3. Они получаются путем введения ограничений  £ [
£ [  ] и
] и  ³ [
³ [  ] + 1 соответственно. Условия задач ЛП-2 и ЛП-3 можно записать следующим образом:
] + 1 соответственно. Условия задач ЛП-2 и ЛП-3 можно записать следующим образом:
ЛП-2

 , , 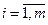 , ,
 , ,  , ,
 , , 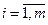 , ,
 £ [ £ [  ] ]
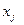 — целые, — целые,  . .
| ЛП-3

 , , 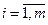 , ,
 , ,  , ,
 , , 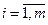 , ,
 ³ [ ³ [  ] + 1 ] + 1
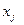 — целые, — целые,  .. ..
|
Допустим, что оптимальные решения задач ЛП-2 и ЛП-3 также содержат дробные значения целочисленных переменных и поэтому не являются допустимыми для исходной задачи.
На следующем шаге необходимо выбрать задачу ЛП-2 или ЛП-3 и произвести ветвление в соответствующей вершине, вводя новое ограничение. Выбор вершины (ЗЛП) для дальнейшего ветвления часто осуществляется с использованием оптимального значения целевой функции, т.е. выбирается вершина, соответствующая наибольшему оптимальному значению целевой функции ЗЛП.
После выбора вершины для дальнейшего ветвления выбирается целочисленная переменная, которая имеет в оптимальном решении соответствующей ЗЛП дробное значение, и производится ветвление по этой переменной. Процесс ветвления и решения ЗЛП продолжается до получения целочисленного оптимального решения одной из ЗЛП. значение Z0 в полученной точке представляет собой текущую нижнюю границу оптимального значения целевой функции исходной задачи ЦЛП. На этом этапе отбрасываются все вершины (ЗЛП), для которых оптимальное значение  не превосходит полученной нижней границы. Про такие вершины также говорят, что они являются прозондированными, поскольку в соответствующих им допустимых областях нет целочисленных решений, лучших, чем уже полученное, следовательно, промежуточная вершина (ЗЛП) является прозондированной (явным или неявным образом) в том случае, если она удовлетворяет хотя бы одному из следующих условий:
не превосходит полученной нижней границы. Про такие вершины также говорят, что они являются прозондированными, поскольку в соответствующих им допустимых областях нет целочисленных решений, лучших, чем уже полученное, следовательно, промежуточная вершина (ЗЛП) является прозондированной (явным или неявным образом) в том случае, если она удовлетворяет хотя бы одному из следующих условий:
1. Оптимальное решение, соответствующее данной вершине, целочисленно.
2. ЗЛП, соответствующая рассматриваемой вершине, не имеет допустимых решений.
3. Оптимальное значение  соответствующей ЗЛП не превосходит текущей нижней границы Z0.
соответствующей ЗЛП не превосходит текущей нижней границы Z0.
Дальнейшее ветвление можно производить только в вершинах, для которых  ³ Z0. Как только полученное допустимое целочисленное решение одной из ЗЛП окажется лучше имеющегося текущего значения Z0, оно фиксируется вместо зафиксированного ранее (т.е. меняется значение Z0).
³ Z0. Как только полученное допустимое целочисленное решение одной из ЗЛП окажется лучше имеющегося текущего значения Z0, оно фиксируется вместо зафиксированного ранее (т.е. меняется значение Z0).
При использовании метода ветвей и границ выбор вершин для дальнейшего ветвления происходит до тех пор, пока остается хотя бы одна непрозондированная вершина. Прозондированная вершина с наилучшим значением Z0 дает решение исходной задачи ЦЛП.
Решить задачу целочисленного программирования методом ветвей и границ, учитывая целочисленность переменных.


Поиск по сайту: