 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Графический способ решения ЗЛП
Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.
Пусть дана задача
 (11)
(11)
 (12)
(12)
 (13)
(13)
Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений (12), (13) задает на плоскости  некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (11) — (13) есть выпуклое множество.
некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (11) — (13) есть выпуклое множество.
Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое множество, например многоугольник  .
.

Выберем произвольное значение целевой функции 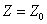 . Получим
. Получим 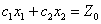 . Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение
. Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение  . Считая в равенстве (11)
. Считая в равенстве (11)  параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
Найдём частные производные целевой функции по 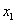 и
и 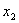 :
:
 , (14)
, (14)
 . (15)
. (15)
Частная производная (14) (так же как и (15)) функции показывает скорость ее возрастания вдоль данной оси. Следовательно,  и
и  — скорости возрастания
— скорости возрастания  соответственно вдоль осей
соответственно вдоль осей  и
и  . Вектор
. Вектор  называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:

Вектор  указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
Вектор  перпендикулярен к прямым
перпендикулярен к прямым  семейства
семейства  .
.
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения.
1. С учетом системы ограничений строим область допустимых решений  .
.
Строим вектор  наискорейшего возрастания целевой функции — вектор градиентного направления.
наискорейшего возрастания целевой функции — вектор градиентного направления.
3. Проводим произвольную линию уровня 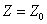 .
.
4. При решении задачи на максимум перемещаем линию уровня 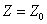 в направлении вектора
в направлении вектора  так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня
так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня 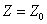 перемещают в антиградиентном направлении.
перемещают в антиградиентном направлении.
5. Определяем оптимальный план  и экстремальное значение целевой функции
и экстремальное значение целевой функции  .
.
Поиск по сайту: