АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задание 4. Решение задач линейного программирования на основе теории двойственности

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.1. Двойственная задача линейного программирования
  6. I. 4.1. Первая теорема двойственности
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. МЕХАНИКА И ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
  11. I. Решение логических задач средствами алгебры логики
  12. I. Розв’язати задачі

Рассмотрим пример построения двойственных задач.

Пусть прямая задача записана в виде основной ЗЛП:

 

Каноническая форма прямой задачи примет вид

Двойственная задача примет вид:

 

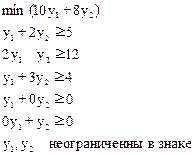
Теоремы двойственности позволяют получить оптимальное решение двойственной задачи по известному оптимальному решению прямой задачи.

Пусть есть прямая ЗЛП:

Пусть известно ее прямое решение

Двойственная задача примет вид:

Т.к. х1 >0, то решение будем искать из первого ограничения двойственной задачи . Т.к. первое и третье ограничение прямой задачи обращается в строгое неравенство при решении прямой задачи, то .

Таким образом, .

Построить двойственные задачи в соответствии с вариантами:

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)