 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задание 2. Решение задач линейного программирования графическим методом
Рассмотрим алгоритм графического метода для ЗЛП, содержащих не более двух переменных и имеющих вид
 (2.1) (2.1)
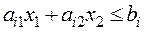 , , 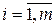 , (1.2) , (1.2)
 , ,  . (2.3)
Алгоритм графического метода рассмотрим на примере применительно к задаче: . (2.3)
Алгоритм графического метода рассмотрим на примере применительно к задаче:
1 шаг. Строим область допустимых решений - область Р, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения ЗЛП. Каждое из неравенств (1-5) системы ограничений нашей задачи геометрически определяет полуплоскость соответственно с граничными прямыми Условия неотрицательности переменных 6) ограничивают область допустимых решений первым квадратом. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных. Построим первую прямую При такой форме записи в знаменатели показаны отрезки, которые отсекает прямая на осях координат, поэтому прямая будет проходить через две точки (0;15) и (15;0). Если от уравнения перейти к неравенству:
Рис. 2.1 Алгоритм построения остальных прямых-ограничений аналогичен и результат построения показан на рис. 2.2.
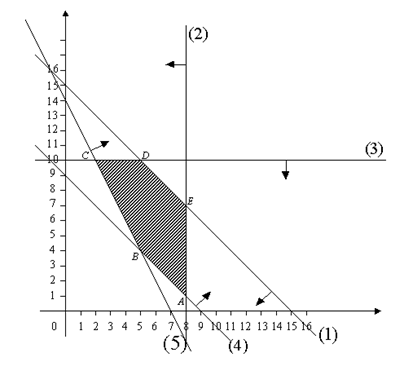
Рис. 2.2
Если система неравенств совместна, то область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Полученное таким образом область допустимых решений Р - планов ЗЛП есть многоугольник ABCDE - замкнутое, ограниченное, выпуклое множество с пятью крайними или угловыми точками: A, B, C, D, E. 2 шаг. Строим вектор 3 шаг. Строим прямую Результаты построений, соответствующие 2 и 3 шагу приведены на рис. 2.3.
Рис. 2.3
4 шаг. Линию уровня целевой функции передвигаем вдоль градиента (в случае её максимизации) или вдоль антиградиента (в случае её минимизации) до тех пор, пока она в какой-нибудь из крайних (или угловых) точек не покинет область Р. Координаты этой точки (функция в ней будет иметь максимальное или минимальное значение) являются оптимальным планом или решением задачи (см. рис. 2.4).
Крайняя точка С - точка минимума лежит на пересечении прямых (3) и (5). Она имеет координаты (2;10), что означает Рис. 2.4
Отметим, что если допустимая область решений Р представляет собой неограниченную область и прямая (линия уровня целевой функции) при движении в направлении вектора  (или противоположном ему) не покидает Р, то в этом случае (или противоположном ему) не покидает Р, то в этом случае  не ограничена сверху (или снизу), т.е. не ограничена сверху (или снизу), т.е.  или или 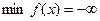 . .
Решить задачу линейного программирования в соответствии с номером в журнале группы. | ||||||||||||||||||



Поиск по сайту:


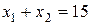 . Для этого запишем уравнение в виде:
. Для этого запишем уравнение в виде:  .
. , то его можно представить графически в виде полуплоскости. Часть плоскости, которая удовлетворяет неравенству, будет лежать по левую сторону от этой прямой, как показано стрелкой. Эта полуплоскость является областью допустимых решений (см. рис. 2.1).
, то его можно представить графически в виде полуплоскости. Часть плоскости, которая удовлетворяет неравенству, будет лежать по левую сторону от этой прямой, как показано стрелкой. Эта полуплоскость является областью допустимых решений (см. рис. 2.1).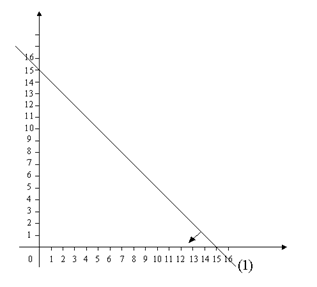
 градиент целевой функции
градиент целевой функции  . В условиях примера
. В условиях примера 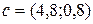 . Напомним, что этот вектор указывает направление возрастания целевой функции.
. Напомним, что этот вектор указывает направление возрастания целевой функции. - линию уровня (т.е. линию, где функция принимает постоянное значение,
- линию уровня (т.е. линию, где функция принимает постоянное значение,  ), перпендикулярную вектору-градиенту
), перпендикулярную вектору-градиенту 
 ,
,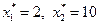 . Подставляя эти значения в целевую функцию, найдем
. Подставляя эти значения в целевую функцию, найдем  .
.