 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Описание первого алгоритма симплекс-метода
Приведём описание алгоритма применительно к ЗЛП, записанной в канонической форме с односторонними ограничениями:

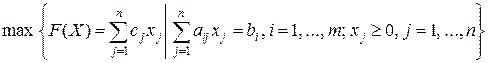
Пусть известен начальный опорный план 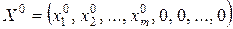 с базисом
с базисом  , т.е.
, т.е.  - базисные компоненты,
- базисные компоненты, 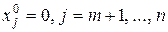 - небазисные компоненты.
- небазисные компоненты.
Вычисления удобно выполнять заполняя следующую симплекс-таблицу:
| C | 
| … | 
| … | 
| ||||
| № | 
| P | B | 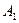
| … | 
| … | 
| t |

| 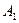
| 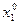
| 
| … | 
| … | 
| ||
| … | … | … | … | … | … | … | … | … | |

| 
| 
| 
| 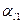
| … | 
| … | 
| 
|
| … | … | … | … | … | … | … | … | … | |

| 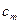
| 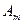
| 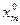
| 
| … | 
| … | 
| |

| 
| 
| … | 
| … | 
|
Порядок вычислений по первому алгоритму:
1. Найти обратную к 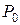 матрицу
матрицу 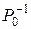 .
.
2. Вычислить коэффициенты разложения векторов условий  по базису
по базису 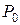 , используя расчётную формулу:
, используя расчётную формулу:

и заполнить ими столбцы  симплекс-таблицы нулевой итерации.
симплекс-таблицы нулевой итерации.
3. Вычислить значение линейной формы  , как скалярное произведение
, как скалярное произведение  соответствующих столбцов симплекс-таблицы, и значения оценок
соответствующих столбцов симплекс-таблицы, и значения оценок 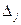 векторов условий
векторов условий  относительно базиса
относительно базиса  в соответствии с формулой
в соответствии с формулой  как скалярное произведение столбцов
как скалярное произведение столбцов 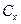 и
и  симплекс-таблицы без коэффициента
симплекс-таблицы без коэффициента  , т.е. по расчётной формуле
, т.е. по расчётной формуле 
Полученными значениями заполнить 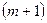 -ю строку симплекс-таблицы.
-ю строку симплекс-таблицы.
4. Проверить оптимальность опорного плана.
· Если  , то
, то  - оптимальный опорный план и, тогда, в столбце
- оптимальный опорный план и, тогда, в столбце  симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
· Если хотя бы в одном столбце с отрицательной оценкой ( ) все элементы меньше или равны 0 (
) все элементы меньше или равны 0 ( ), то линейная форма
), то линейная форма  не ограничена сверху и решения ЗЛП не существует. На этом процесс решения ЗЛП также завершается.
не ограничена сверху и решения ЗЛП не существует. На этом процесс решения ЗЛП также завершается.
· Если же в каждом столбце с отрицательными оценками найдется хотя бы один положительный элемент  , то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки
, то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки  и, таким образом, определяется разрешающий столбец
и, таким образом, определяется разрешающий столбец 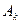 .
.
5. Определить вектор, исключаемый из базиса для чего необходимо заполнить последний столбец 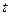 симплекс-таблицы нулевой итерации путем деления элементов столбца
симплекс-таблицы нулевой итерации путем деления элементов столбца  на соответствующие им по номеру элементы разрешающего столбца
на соответствующие им по номеру элементы разрешающего столбца 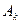 , т.е.
, т.е. 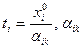 >0,
>0,
При этом, в строках столбца 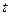 , соответствующих неположительным элементам
, соответствующих неположительным элементам  , записываем
, записываем  , не выполняя деления.
, не выполняя деления.
Далее необходимо выбрать  . Если
. Если  достигается на нескольких позициях столбца
достигается на нескольких позициях столбца 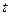 , то из базиса может быть исключен любой из векторов
, то из базиса может быть исключен любой из векторов  Для определенности, договоримся исключать из них вектор с наименьшим номером.
Для определенности, договоримся исключать из них вектор с наименьшим номером.
Пусть  получился на
получился на  -той позиции, т.е.
-той позиции, т.е. 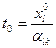 , тогда соответствующий этому индексу вектор
, тогда соответствующий этому индексу вектор  должен выводиться из базиса. Строка симплекс-таблицы, соответствующая этому индексу, называется разрешающей строкой. Элемент
должен выводиться из базиса. Строка симплекс-таблицы, соответствующая этому индексу, называется разрешающей строкой. Элемент  , стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
, стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
6. Заполнить новую симплекс-таблицу в следующей последовательности.
6.1. На  -тых позициях столбцов
-тых позициях столбцов 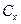 и
и 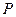 записать соответственно
записать соответственно  и
и 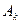 , а на остальных позициях этих столбцов оставить прежние элементы.
, а на остальных позициях этих столбцов оставить прежние элементы.
6.2. Заполнить 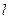 -тую строку новой симплекс-таблицы элементами
-тую строку новой симплекс-таблицы элементами  ,
,  , получающимися делением соответствующих элементов (
, получающимися делением соответствующих элементов (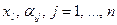 )
)  -той строки старой симплекс-таблицы на разрешающий элемент
-той строки старой симплекс-таблицы на разрешающий элемент  , т.е. по формулам
, т.е. по формулам  .
.
6.3. Все остальные 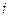 -тые строки главной части новой симплекс-таблицы получить как результат вычитания из
-тые строки главной части новой симплекс-таблицы получить как результат вычитания из 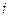 -той строки старой симплекс-таблицы
-той строки старой симплекс-таблицы  -той строки новой симплекс-таблицы, умноженной на соответствующий
-той строки новой симплекс-таблицы, умноженной на соответствующий 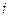 -тый элемент разрешающего столбца, т.е. в соответствии с рекуррентными формулами
-тый элемент разрешающего столбца, т.е. в соответствии с рекуррентными формулами  . По аналогичным формулам вычисляются также и элементы
. По аналогичным формулам вычисляются также и элементы  -й строки новой таблицы:
-й строки новой таблицы: 
Этим завершается построение новой симплекс-таблицы.
Описанный процесс построения симплекс-таблиц повторяется до получения оптимального опорного плана или до установления неограниченности линейной формы, т.е. неразрешимости ЗЛП.
Если среди оценок 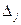 небазисных векторов условий
небазисных векторов условий  относительно базиса найденного оптимального опорного плана найдется хотя бы одна равная нулю, то это означает, что ЗЛП имеет неединственное решение.
относительно базиса найденного оптимального опорного плана найдется хотя бы одна равная нулю, то это означает, что ЗЛП имеет неединственное решение.
Поиск по сайту: