АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка двойственной задачи

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Ситуационные задачи и тестовые задания.
  9. I. Цель и задачи дисциплины
  10. I.5.3. Подготовка данных для задачи линейного программирования
  11. I.5.4. Решение задачи линейного программирования
  12. I.5.5. Просмотр и анализ результатов решения задачи

Любой задаче линейного программирования определённым образом соответствует некоторая другая задача линейного программирования, называемая двойственной или сопряженной. Первоначальная задач называется исходной или прямой. Тесная связь между исходной и двойственной задачами, составляющими так называемую двойственную пару, проявляется в том, что, зная решение одной из этих задач, можно построить решение другой на основании теоремы о двойственности. Запишем задачи двойственной пары в случае рассматриваемой нами прикладной задачи.

Введём обозначения: ; ;

; ; (2.29)

Нашу исходную задачу (2.5) – (2.7) сформулируем, используя матричную форму записи, следующим образом: требуется определить вектор , обращающий в максимум функцию

(2.30)

при условиях

; (2.31)
. (2.32)

Тогда двойственная задача формулируется так: определить вектор , обращающий в минимум функцию

(2.33)

при условии

. (2.34)

Целевая функция (2.33) двойственной задачи может быть записана в эквивалентной форме:

(2.35)

Транспонируя обе части неравенства (2.34), записанного в виде строки, и учитывая что , ограничения (2.34) двойственной задачи получим в виде

(2.36)

Отметим, что в двойственной задаче переменные могут быть и отрицательными.

Таким образом, для получения двойственной задачи из прямой необходимо выполнить следующие действия:

- транспонировать векторы ограничений и коэффициентов линейной формы и поменять их местами;

- транспонировать матрицу условий ;

- заменить знаки равенства в ограничениях (2.31) знаками неравенств ;

- исключить условия неотрицательности (2.32);

- заменить требование максимизации целевой функции требованием её минимизации.

Выполним эти действия применительно к рассматриваемой нами исходной задаче (2.15), (2.16). Применительно к ней матрицы (2.29) запишутся так:

, ,

 

;

 

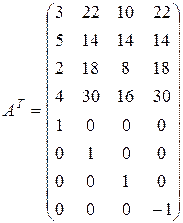Двойственная задача имеет вид

(2.37)

(2.38)

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)