 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Математическая постановка задачи. Для того чтобы решить предложенную задачу с использованием результатов и вычислительных процедур теории оптимизации
Для того чтобы решить предложенную задачу с использованием результатов и вычислительных процедур теории оптимизации, необходимо сформулировать рассматриваемую задачу на математическом языке, то есть построить математическую модель оптимизации.
Обозначим через  количество товара
количество товара 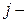 того вида
того вида 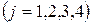 , производимого на предприятии за определённый промежуток времени. Значения этих величин и следует определить исходя из условия достижения предприятием максимальной экономической эффективности.
, производимого на предприятии за определённый промежуток времени. Значения этих величин и следует определить исходя из условия достижения предприятием максимальной экономической эффективности.
Экономическую эффективность в рассматриваемой задаче предлагается оценивать величиной прибыли, получаемой от реализации всего произведённого товара. Так как прибыль, получаемая от реализации единицы товара каждого вида известна (см.таблицу 1.1), то общая прибыль с учётом введённых обозначений может быть вычислена как значение следующей целевой функции
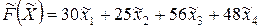 (2.1)
(2.1)
Составим систему неравенств, учитывающих ограниченность ресурсов, которыми располагает предприятие.
Количество ресурса каждого вида (сырьё, рабочая сила, оборудование), расходуемое на изготовление товаров всех наименований, не может превышать имеющегося запаса данного ресурса. Эти ограничения запишем в виде следующих трёх неравенств:
 (2.2)
(2.2)
Суммарные трудовые затраты на изготовление товаров всех наименований не должны быть меньше заданного по условию технической постановки значения (см.таблицу 1.1). Это ограничение запишем в виде неравенства:
 (2.3)
(2.3)
Количество изделий каждого наименования, которое необходимо изготовить, не должно быть меньше заданного по условию технической постановки минимально необходимого значения. Данное ограничение, наложенное непосредственно на значения искомых переменных, запишем в виде неравенств:
 (2.4)
(2.4)
В результате проведённых действий предложенная прикладная задача математически поставлена как задача линейного программирования (ЗЛП):
Требуется найти значения переменных  , доставляющие максимум целевой функции
, доставляющие максимум целевой функции 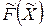 (2.1) и удовлетворяющие ограничениям (2.2) - (2.4).
(2.1) и удовлетворяющие ограничениям (2.2) - (2.4).
Поиск по сайту: