Решение исходной задачи

Весь процесс решения исходной задачи (2.15) – (2.16) приведен в таблице 4.1.

Заполнение таблицы, отвечающей 0-й итерации, происходит на основе таблицы 2.1 (см. итерацию 1) следующим образом. Главная часть таблицы 0-й итерации исходной задачи (за исключением (m +1)-й строки) полностью повторяет главную часть таблицы заключительной итерации L -задачи без столбца 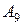. Также без изменений остается столбец Р базисных векторов. Строка коэффициентов линейной формы исходной задачи и столбец коэффициентов при базисных переменных заполняются исходя из (2.15). С учетом новых элементов столбца 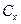пересчитываются значение линейной формы и оценки .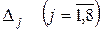

Заполнение таблиц, отвечающих последующим итерациям, происходит в соответствии с описанным выше алгоритмом.

Таблица 2.2

0 итерация

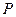
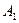
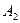
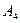
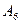
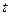
44 1/3

1/15

3 2/15

-2/5

2/15

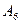
79 1/3

-1 11/15

6 8/15

-1 3/5

8/15

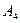
1 2/3

11/15

7/15

3/5

-1/30

2 7/9

m+1

-

-

5 1/5

-2 3/5

-27 1/5

-1 3/5

-

1 итерация

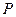
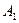
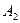
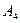
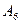
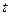
45 4/9

5/9

3 4/9

2/3

1/9

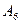
83 7/9

2/9

7 7/9

2 2/3

4/9

188 1/2

2 7/9

1 2/9

7/9

1 2/3

-1/18

m+1

-

-

155 5/9

38 4/9

18 5/9

45 1/3

-3 1/9

-

2 итерация

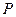
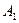
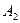
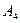
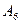
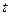
24 1/2

1/2

1 1/2

-1/4

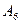
29 1/2

-1/2

-17 1/2

-6

-2 1/4

188 1/2

1/2

17 1/2

2 1/4

13 1/4

1 1/4

1 3/4

1/8

m+1

-

-

-

Решение ЗЛП (2.15) – (2.16) получено за две итерации. Оптимальным планом её является вектор 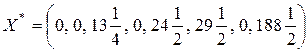и .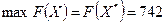

Вернемся к исходной задаче (2.1) – (2.2) со старыми переменными 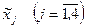. Из (2.7) и (2.11) получим

(2.22)

и

. (2.23)

Принимая во внимание, что переменные 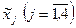могут принимать только натуральные значения, можем сказать, что при заданных затратах ресурсов на изготовление единицы товара, известных запасах ресурсов и прибыли на единицу товара предприятию необходимо выпускать следующий ассортимент товаров: 2 изделия №1, 3 изделия №2, 15 изделий №3, 1 изделие №4. Максимальная прибыль при этом составит 1023 у.е.

Формирование М -задачи

Далеко не всегда имеет смысл разделять решение задачи линейного программирования на два этапа – вычисление начального опорного плана и определение оптимального плана. Вместо этого решается расширенная задача (М -задача). Она имеет другие опорные планы (один из них всегда легко указать), но те же решения (оптимальные планы), что и исходная задача.

Расширенная М-задача применительно к исходной задаче (2.5) – (2.7) записывается следующим образом:

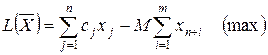;	(2.24)
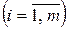;	(2.25)
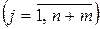.	(2.26)

Здесь 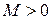- достаточно большое число.

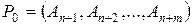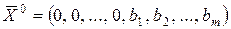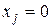
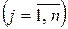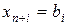
Начальный опорный план задачи (2.24) – (2.26) может быть назначен непосредственно, так как в матрице условий этой задачи уже сформирована единичная подматрица, которая и составит его базис . Поэтому вектор с компонентами , 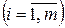и будет являться начальным опорным планом задачи (2.24) – (2.26).Переменные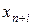 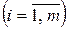называются искусственными переменными.

Таким образом, исходная задача линейного программирования с неизвестным заранее начальным опорным планом сводится к М -задаче, начальный опорный план которой может быть указан непосредственно. В процессе решения этой расширенной задачи можно либо вычислить оптимальный план задачи (2.5) – (2.7), либо убедиться в её неразрешимости, если оказывается неразрешимой М -задача.

В соответствии с вышеизложенным составим М - задачу применительно к нашей ЗЛП (2.15), (2.16), записанной в канонической форме. Для этого введём одну искусственную неотрицательную переменную 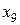и запишем М -задачу в виде:

	(2.27)
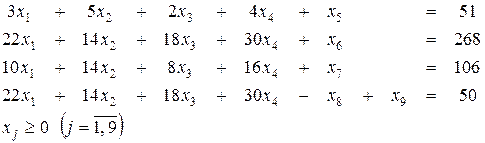
	(2.28)

где М – сколь угодно большая положительная величина. Считается что она заведомо больше любого числа которыми будут заполняться симплекс-таблицы.

Замечание: как и в L -задаче, добавление только одной искусственной переменной 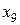(вместо четырёх) обусловлено тем, что исходная задача уже содержит три единичных вектора условий .

Решение М -задачи вторым алгоритмом симплекс-метода

Поиск по сайту: