Приведение задачи к канонической форме

Задача линейного программирования записана в канонической форме, если она формулируется следующим образом.

Требуется найти вектор , доставляющий максимум линейной форме

(2.5)

при условиях

(2.6)   (2.7)

где .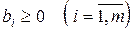

То есть, в канонической форме ЗЛП обязательным является требование максимизации целевой функции (2.5), ограничения задачи должны быть записаны в виде системы линейных алгебраических уравнений (2.6) с неотрицательными правыми частями, а на искомые переменные должны быть наложены условия неотрицательности (2.7).

Нами сформулирована исходная ЗЛП (2.1) - (2.4):

	(2.8)
	(2.9)   (2.10)

Для приведения поставленной нами ЗЛП (2.8)-(2.10) к канонической форме необходимо все ограничения (2.9)-(2.10) преобразовать к виду равенств с помощью введения дополнительных неотрицательных переменных.

Число ограничений задачи, приводящих к уравнениям вида (2.6) в нашем случае можно уменьшить, если преобразовать неравенства (2.10) к виду (2.7) используя замену переменных. Для этого перенесем свободные члены правых частей неравенств (2.10) в левые части и введём новые переменные

Выразим теперь старые переменные через новые

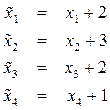
и подставим их в линейную форму (2.8) и систему неравенств (2.9). Получим

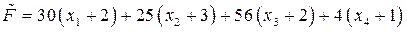
Раскрывая скобки и учитывая, что

(2.11)

запишем исходную задачу так:

	(2.12)
	(2.13)
	(2.14)

Для записи неравенств (2.13) в виде уравнений введем неотрицательные переменные , добавляя их в левые части первых трёх неравенств со знаком плюс, а в левую часть последнего неравенства со знаком минус. Тогда задача (2.12) - (2.14) запишется в следующей эквивалентной форме:

	(2.15)
.	(2.16)

Задача (2.15), (2.16) и есть исходная ЗЛП в канонической форме.

Нахождение начального опорного плана

Метод последовательного улучшения плана (так называемый симплекс-метод), который применяется для решения сформулированной ЗЛП (2.15)-(2.16), предполагает знание некоторого исходного опорного плана. Однако, далеко не всегда такой начальный опорный план может быть указан без каких-либо вычислений. Это возможно лишь в случае, когда среди столбцов матрицы условий найдётся достаточное количество таких столбцов, из которых составится единичная матрица и эта матрица будет являться базисом искомого начального плана.

Если же такой возможности нет, то для построения начального опорного плана исходной ЗЛП (2.5)-(2.7) решается вспомогательная ЗЛП (так называемая задача) с расширенным вектором , состоящим из вектора 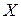исходной ЗЛП, дополненного искусственными неотрицательными компонентами Последние вводятся в систему ограничений (2.16) так, чтобы сформировался искусственный единичный базис.

Итак, начальный опорный план задачи (2.5) - (2.7) может быть найден с помощью следующей вспомогательной ЗЛП (L - задачи):

	(2.17)
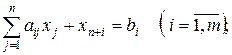
	(2.18)
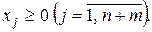
	(2.19)

Так как матрица условий ЗЛП (2.17)-(2.19) уже содержит единичную подматрицу которая может быть взята в качестве базиса опорного плана, то начальным опорным планом этой задачи будет являться вектор

,

у которого небазисные компоненты а базисные

Решая сформулированную задачу, например, первым алгоритмом симплекс- метода (описание алгоритма приводится ниже в п.4), с указанным начальным планом , в силу ограниченности линейной формы сверху на множестве своих планов () окажется, что процесс решения через конечное шагов приведет к оптимальному опорному плану вспомогательной задачи.

Пуст - оптимальный опорный план 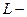задачи, у которого все искусственные компоненты равны нулю. Тогда вектор является опорным планом исходной задачи. Действительно, все дополнительные переменные . Значит, компоненты вектора удовлетворяют ограничениям исходной задачи, т.е. вектор является некоторым планом задачи (2.5) - (2.7). По построению план является также опорным.

Постановка L - задачи

В нашем случае ЗЛП (2.15)-(2.16) имеет матрицу условий

Она уже содержит три столбца которые можно использовать для построения единичного базиса. Недостаёт лишь одного столбца. Поэтому в нашем случае следует ввести только одну неотрицательную искусственную переменную в левую часть четвёртого уравнения системы ограничений (2.16). Тогда вспомогательная задача для нахождения начального опорного плана задачи (2.15) - (2.16) запишется так:

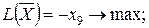
	(2.20)
	(2.21)

Определим начальный опорный план полученной 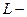задачи. При постановке этой задачи сформирован единичный базис 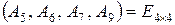искомого начального опорного плана 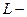задачи. Его компоненты являются небазисными и поэтому приравниваются нулю. Тогда из системы ограничений (2.21) найдутся значения базисных компонент

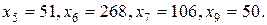
Итак, в качестве начального опорного плана задачи может быть взят вектор

Решение L - задачи

Решение L - задачи будем проводить в соответствии с первым алгоритмом симплекс-метода (описание алгоритма приводится ниже). Составим таблицу, соответствующую исходному опорному плану (0-й итерации). Так как - базис начального опорного плана , является единичной матрицей, то обратная матрица 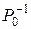также является единичной и поэтому коэффициентами разложения векторов условий по этому базису 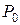являются коэффициенты системы (2.21).

Для заполнения -й строки симплекс-таблицы вычислим значения линейной формы 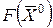и оценок , векторов условий по приведённым в описании первого алгоритма формулам (см. раздел 4) следующим образом:

Весь процесс решения приведен в табл. 3.1, которая состоит из двух частей, отвечающих 0-й (исходная таблица) и 1-й итерациям.

Заполняем таблицу 0-й итерации.

Среди оценок имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису путём операции однократного замещения. В базис будет введён вектор с наименьшей оценкой . Значения 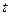вычисляются для всех позиций столбца 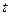(так как все элементы разрешающего столбца положительны). Наименьший элемент 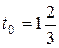достигается на четвертой позиции базиса. Значит, четвертая строка является разрешающей строкой, и вектор подлежит исключению из базиса.

Составим таблицу, отвечающую первой итерации.

В столбце 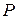, в четвертой позиции место вектора 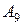займёт вектор . Соответствующий ему коэффициент линейной формы помещаем в четвертой позиции столбца . Главная часть таблицы 1 заполняется по данным таблицы 0 в соответствии с рекуррентными формулами. Так как после завершения первой итерации все оценки , то полученный опорный план является оптимальным опорным планом L - задачи. Максимальное значение линейной формы задачи равно нулю .

Таблица 2.1

0 итерация

										-1
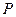
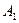
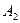
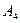
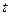
													12 3/4
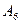
													8 4/15
													6 5/8
	-1										-1		1 2/3
m+1	-	-	-50	-22	-14	-18	-30

1 итерация

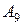
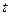
44 1/3

1/15

3 2/15

-2/5

2/15

-2/15

-1

79 1/3

-1 11/15

6 8/15

-1 3/5

8/15

-8/15

1 2/3

11/15

7/15

3/5

-1/30

1/30

m+1

-

-

Формирование начального опорного плана исходной ЗЛП

Искусственная компонента найденного в п.3.2 оптимального опорного плана задачи равна нулю =0. Поэтому, как видно из сравнения ограничений (2.21) и (2.16), компоненты удовлетворяют ограничениям исходной ЗЛП. Следовательно вектор является планом исходной задачи (2.15) – (2.16). Кроме того, он является также опорным планом. Поэтому он может быть выбран в качестве начального опорного плана задачи (2.15) – (2.16).

Таким образом найден начальный опорный план исходной ЗЛП: .

Поиск по сайту: