АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формирование решения двойственной задачи

Читайте также:
  1. FAST (Методика быстрого анализа решения)
  2. I Психологические принципы, задачи и функции социальной работы
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Формирование глобального инновационного общества
  11. I. Формирование системы военной психологии в России.
  12. I. Цель и задачи дисциплины

Для формирования решения двойственной задачи воспользуемся следующей теоремой.

Основная теорема о двойственности. Если одна из задач двойственной пары (2.30) – (2.32) и (2.35) - (2.36) имеет решение, то другая задача также разрешима. При этом для любых оптимальных планов 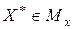и 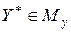(здесь , - множества планов соответственно прямой и двойственной задач) задач (2.30) – (2.32) и (2.35) - (2.36) имеет место равенство .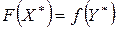

Если же линейная форма одной из задач не ограничена (для - сверху, для - снизу), т.е. не имеет решения, то другая задача не имеет ни одного плана, т.е. также неразрешима.

Оптимальное решение двойственной задачи может быть найдено на основе следующего следствия из этой теоремы.

Следствие. Если вектор является оптимальным опорным планом задачи (2.30) – (2.32), то вектор

(2.39)

является оптимальным опорным планом задачи (2.33), (2.34).

Напомним, что в ходе решения исходной задачи вторым алгоритмом, на каждой итерации вычисляется вектор 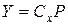. И если 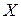- оптимальный опорный план задачи (2.30) – (2.32), то в (m+1)-й строке, соответствующей основной таблице, находится решение задачи (2.35)- (2.36).

Итак наша двойственная задача имеет вид (2.37)- (2.38).

Так как исходная задача (2.15), (2.16) имеет решение, то на основании рассмотренной теоремы о двойственности двойственная задача также разрешима.

Оптимальным опорным планом исходной задачи является вектор. При этом 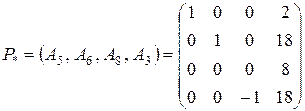; ; . Обратная матрица принимает вид .

В силу следствия из теоремы о двойственности можно заключить, что вектор-строка 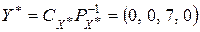является оптимальным планом двойственной задачи, при котором 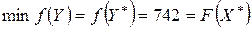. Анализируя (m +1)-ю строку основной таблицы (см. табл. 6.1, шаг 3), можно убедиться в том, что оптимальный план двойственной задачи, сформированный на основе теоремы о двойственности, совпадает с оптимальным планом, найденным при решении исходной задачи вторым алгоритмом симплекс-метода. Это говорит о том, что оптимальный план двойственной задачи (2.37) – (2.38) найден, очевидно, верно.


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)