Метод множителей Лагранжа

Рассмотрим частный случай общей задачи нелинейного программирования (1), (2), предполагая, что система огра­ничений (2) содержит только уравнения, отсутствуют усло­вия неотрицательности переменных и функции f и g_i - непрерывные вместе со своими частными производными

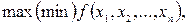(1)

(2)

В курсе математического анализа задачу (1), (2) назы­вают задачей на условный экстремум или классической задачей оптимизации.

Чтобы найти решение такой задачи, вводят набор пере­менных называемых множителями Лагранжа, и составляют функцию Лагранжа:

(3)

находят частные производные и , рассматривают систему n+m уравнений:

(4)

с n+m неизвестными . Всякое решение системы (4) определяет точку в которой может иметь место экстремум функции . Следовательно, решив систему (4), получают все точки, в которых функция (1) может иметь экстремальные значения. Дальнейшее исследование найденных точек про­водят так же, как и в случае безусловного экстремума.

Пример. Известен рыночный спрос на определенное изде­лие в количестве 180 штук. Это изделие может быть изготов­лено двумя предприятиями одного концерна по различным технологиям. При производстве х₁ изделий первым предприя­тием его затраты составят 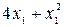руб., а при изготовлении х₂ изделий вторым предприятием они составляют 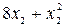руб.

Определить, сколько изделий, изготовленных по каж­дой технологии, может предложить концерн, чтобы общие издержки его производства были минимальны.

Решение. Задача запишется в виде:

(5)

(6), (7)

Для нахождения минимального значения функции (5) при условии (6), т. е. без учета требования неотрицательно­сти переменных, составляется функция Лагранжа:

вычисляются ее частные производные по и приравнивается нулю:

Отсюда или . Решая это уравнение совместно с , находим , т. е. получаем координаты точки, подозрительной на экстремум. Используя вторые частные производные, можно показать, что в этой точке функция f имеет услов­ный минимум.

Такой же результат можно получить, если исследова­ние на условный экстремум функции f свести к исследова­нию на безусловный экстремум функции f _1? полученной из f в результате ее преобразований.

Таким образом, если из уравнения связи найти х₂ = 180 – x₁ и подставить это выражение в целевой функции, то получится функция одной переменной x₁.

.

или 4х₁ - 364 = 0, откуда . Ис­пользуя вторые частные производные, устанавливаем, что в данной точке функция f имеет минимальное значение.

Поиск по сайту: