Графический метод решения задач линейного программирования

Вспомним построение линейных зависимостей. Начнем с уравнений. Линейное уравнение с двумя переменными может быть записано . Чтобы построить это уравнение, найдем точки пересечения с осями координат.

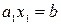При x₁ =0 получим , откуда . При х₂= 0 будем иметь и (рис. 2).

Разделим теперь левую и правую части уравнения на b и перепишем уравнение, которое называют уравнением пря­мой в отрезках:

Рис. 2

Такое представление уравнения удобно для построения прямой, так
как величины α₁ и α₂ - это отрезки, отсекаемые прямой на тех осях, которые указаны в числи­теле. Например, или в форме уравнения в от­резках:

т.е. α₁ = 1, α₂ = 2.

Теперь о неравенствах. Если линейное уравнение с дву­мя переменными может быть представлено прямой на плоскости, то неравенство изоб­ражается как полуплоскость.

Так, неравенство представляет собой за­штрихованную полуплоскость, координаты всех точек кото­рой, т. е. х₁ и х₂, удовлетворяют заданному равенству. Зна­чит, эти значения составляют область допустимых реше­ний (рис. 3).

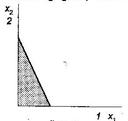
Рис. 3

Рассмотрим построение системы линейных неравенств:

или в форме, аналогичной уравнениям в отрезках:

Построим каждое неравенство в системе координат х₁, х₂ в виде соответствующих полуплоскостей. Решение этой системы неравенств - координаты всех то­чек, принадлежащих области допустимых решений, т.е. АВСDО.

Так как в области допустимых решений бесчисленное множество точек, значит, рассматриваемая задача имеет бесчисленное множество допустимых решений (рис. 4).

Рис. 4 Рис. 5

Не любая система линейных неравенств имеет об­ласть допустимых решений, т.е. допустимые решения.

Например, построим систему:

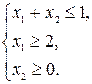
Из рис. 5 видно, что нет таких точек, которые бы удовлетворяли всем неравенствам системы.

Итак, мы рассмотрели линейные уравнения и неравен­ства с двумя переменными. Если перейти к линейным за­висимостям с тремя переменными, то тогда они будут опи­сывать плоскость в трехмерном пространстве; линейное неравенство характеризует полупространство, а система линейных неравенств - многогранник как область допу­стимых решений в трехмерном пространстве.

С увеличением числа переменных выше трех геометри­ческая интерпретация невозможна, так как система нера­венств - область допустимых решений в k -мерном про­странстве.

При этом мерность пространства определяют так: если ограничения заданы неравенствами, то k = n и, где п - чис­ло переменных; если ограничения в виде уравнений, то k = n - т, где т - число уравнений.

Если необходимо найти оптимальное решение, то сле­дует принять целевую функцию. Допустим, мы хотим, что­бы решение было оптимальным в смысле максимизации выпуска в целом. Тогда целевая функция:

Положим L, равной какому-либо числу (любому), на­пример 2, и построим уравнение целевой функции:

Так как нам требуется найти оптимальное решение, при котором достигается mах L, будем перемещать линию целевой функции в направлении увеличения L. Очевидно, что оптимальным решением будут координаты точки С, равные 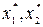. При этом L = L*.

Отсюда можно сделать исключительно важный вы­вод: оптимальное решение - координаты вершины облас­ти допустимых решений.

Из этого вывода следует метод решения задач линейно­го программирования, который заключается в поиске вер­шин области допустимых решений как точки пересечения ограничений; последовательном определении значения це­левой функции в вершинах.

Вершина, в которой целевая функция приобретает оп­тимальное (максимальное или минимальное) значение, яв­ляется оптимальной вершиной.

Координаты оптимальной вершины есть оптимальные значения искомых переменных.

Поиск по сайту: