Оптимальные решения при ограничениях-неравенствах. Теорема Куна - Таккера

Изученные особенности функции позволяют сформулировать положения, относящиеся непосредственно к нелинейным, задачам математического программирования. Пусть дана задача: найти

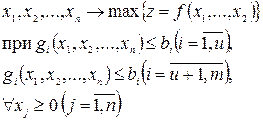(1)

Все предположения относительно z и gi , вы­двинутые выше, сохраняются здесь полностью. Требуется получить условия существования решений, основанные на введенных понятиях.

Чтобы избежать неудобств, связанных с присутствием в (1) ограничений-неравенств и требований неотрицательноcти переменных x_j, представим (1) в эквива­лентной форме

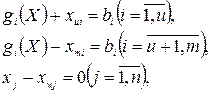(2)

где - вспомогательные переменные, по­зволяющие формально исключить знаки «≤, ≥» (1). Для этого случая, функция Лагранжа запишется как

а необходимые условия, которым должны удовле­творять оптимальные 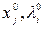, принимают обычный вид

Рассмотрим более подробно равенства

Их можно представить как

(3)

собрав под знаком Σ производные по х_j первых, двух сумм выражения 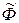. Ясно, что появление здесь слагае­мого есть следствие перехода от системы (1) к (2). Обратим теперь.внимание на то, что в левую часть (3) входит выражение производной по х_j. Функции

т.е. функции Лагранжа в ее классическом виде. Для cоставления достаточно данных исходной задачи (1), поэтому естественно стремиться сформулировать такие условия существования экстремума f(X),которые включали бы только , а не .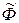

Обратим внимание на множитель , связанный с j -й искусственной строкой (2) и обладающий свойст­вом 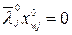. При (или, что то же, при ) он обращается в нуль, и необходимые условия сущест­вования Х⁰ (из рассматриваемых в данный момент) принимают вид

Далее, при 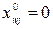(это равносильно равенству 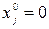, так как ) соответствующий множитель отличен, вообще говоря, от нуля. Его знак в этом случае определяется из следующих соображений: если правой, части любой строки дать отрицательное при­ращение, то область определения исследуемой задачи только расширится (произвольное значение удо­влетворяет и неравенству ); величина z⁰ при этом не уменьшится (всякое расширение U, создает предпосылки для улучшения ожидаемых z⁰), т.е. или . Таким образом, при 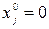необ­ходимые условия есть

Обращаясь теперь к группе соотношений 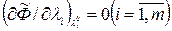и применяя те же способы оценки знаков 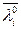, можно получить, объединенную сводку искомых не­обходимых условий, которым должны удовлетворять оптимальные 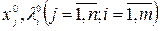в рассматриваемой задаче (1):

(4)

Следует специально подчеркнуть, что соотношения (4) должны рассматриваться лишь тогда, когда существуют такие , при которых 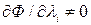, т.е. ; в противном случае возникает неопределенность выбора (нару­шается условие регулярности ограничений (1), мно­жество компонент 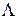становится неограниченным), и равенства 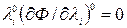теряют смысл.

Очевидно, требования (4) полностью совпадают с (1) (п. 4.3) при Х≥0, причем соответствие результатов рас­пространяется и на достаточные условия существования .

Пусть точка удовлетворяющая (4), является седловой для ; следовательно, должно выпол­няться неравенство

В силу (4) сумма 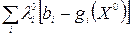равна нулю, а каждое слагаемое суммы 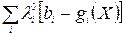неотрицательно поскольку знаки разностей 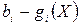в (1) и соответ­ствующих в (4) всегда совпадают. Таким образом, приходим к утверждению «f(X) + (неотрицательная ве­личина) ≤ f(X⁰)» и тем более . Этим под­тверждается достаточность исходного предположения.

Проведенный анализ свойств экстремума z в задаче (1) позволяет дать краткую формулировку теоремы Куна - Таккера: для того, чтобы экстремум функции f(X) был достигнут в точке при условиях (1), необходимо и достаточно требовать су­ществования таких , при которых является седловой точкой функции .

Заметим теперь, что теорема Куна - Таккера, отра­жающая роль седловой точки , может рассматри­ваться с более общих позиций, вне связи с предположениями о дифференцируемости .

Пусть, например, в задаче (1) отсутствуют требо­вания, существования производных и некоторая точка является седловой для функ­ции

на множестве U, причем 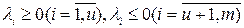. Нетрудно убедиться, что эти условия являют­ся достаточными условиями экстремума, (в данном слу­чае максимума). Действительно, из определения седловой точки следует

;

правое неравенство есть

или

;

поскольку знаки 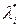, совпадают со знаками соответствующих разностей , и кроме того, рассматри­ваемое неравенство выполняется для всех допустимых (в частности, для ), получаем ; в этой ситуации левое неравенство принимает вид f(X) + (неотрицательная величина) ≤ f(Х*) или f(X) ≤ f(Х*), что и подтверждает опти­мальность X*.

Таким образом, использование производных функции в ходе доказательств теорем о существований экстремума совсем не обязательно, однако в инженер­ных задачах оно часто приводит к упрощениям рас­четов.

В заключение полезно подвести некоторые итоги: ис­следована проблема обобщения классического метода множителей Лагранжа на случай ограничений вида и Х≥0 в задачах нелинейного программиро­вания; показана возможность такого обобщения и изу­чены особенности функции Лагранжа в точке относительного экстремума f(X); установлена связь между условиями существования точек X⁰ и , вы­раженная теоремой Куна - Таккера. Ниже дан пример •непосредственного использования полученных результа­тов.

Пример. Найти

при

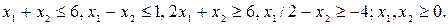
Решение. Составим функцию Лагранжа в ее классическом виде (так, как это было бы в случае ограничений-равенств отсутствия требований неотрицательности х₁, х₂):

Из условий и 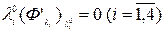получаем

Среди возможных решений этой системы нужно выбрать теперь те, которые удовлетворяют соотношениям (4). Оказывается, этим свойством обладает одно решение:

тот факт, что все 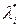оказались равными нулю, а , указывает на несущественность исходных ограничений зада­чи; проверка достаточных условий сводится к установлению факта выпуклости z (это можно сделать здесь простыми геометрическими построениями).

Теория Куна - Таккера позволяет заметно расширить круг задач нелинейного программирования, решение ко­торых может быть получено в аналитическом виде.

Поиск по сайту: