Общая постановка задачи динамического программирования

До сих пор рассматривались такие задачи оптимиза­ции, в которых принятие решения осуществлялось в один этап. Зависимость рассматриваемого этапа от прошлого и его влияние на будущее не учитывалось.

В реальных задачах управления приходится принимать и реализовывать решения по нескольким этапам. Такие задачи многоэтапной оптимизации называют задачами ди­намического программирования (ДП), в том числе:

-распределение ресурсов, например, ограниченного объе­ма капиталовложений между возможными направле­ниями их использования по объему и времени;

-разработка правил управления запасами, устанавливаю­щих момент пополнения и размер пополняемого запаса;

-выбор транспортных маршрутов или технологических способов изготовления изделий;

-разработка принципов календарного планирования про­изводства.

Условность задач линейного программирования приме­нительно к управлению состоит в оптимизации только для какой-то стационарной ситуации. В действительности за­дачи управления динамичны, поэтому точнее определять оптимум не для одного момента времени, а последователь­но на протяжении длительного периода.

Например, недостаточно определить оптимальный план производства на месяц, вполне вероятно, что в последую­щие месяцы производство может быть неоптимальным, так как возможности дальнейшего развития не учитывались. Составление ежемесячных оптимальных планов более эф­фективно с учетом предшествующих периодов, так как го­довой оптимальный план будет результатом оптимальных решений, принятых для каждого месяца; причем план каж­дого последующего месяца должен учитывать решения, принятые в предыдущих.

Динамическое программирование дает возможность при­нять ряд последовательных решений (многошаговый процесс), обеспечивающих оптимальность развития процесса в целом.

В задачах динамического программирования рассматривается управляемая система, которая под влиянием управле­ния переходит из начального состояния в конечное состояние . Пред­положим, что процесс управления системой можно разбить на n шагов. Пусть - состояния системы после 1-го, 2-го,..., n -го-шагов. Состояние системы после k- гошага характеризуется пара­метрами 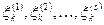, которые называются фазовыми координатами. Состояние можно изобразить точкой s -мерного пространства, называемого фазовым. Последовательное преобразование системы (по шагам) достигает­ся с помощью некоторых мероприятий , которые составляют управление системой , где - управление на k- м шаге, переводящее систему из состояния в состояние . Управление на k- м шаге заключается в выборе значений определенных управляющих пе­ременных . Предполагаем, что состояние системы в кон­це k -гошага зависит только от предшествующего состояния системы и управления на данном шаге. Такое свойство получило название отсутствие последействия. Запишем эту зависимость в виде

(1)

Равенства (1) получили название уравнений состояний.

Варьируя управление U, получим различную эффективность процесса, которую будем оценивать количественно-целевой функцией

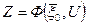(2)

Показатель эффективности k -го шага процесса управления, который зависит от состояния в начале этого шага и управления , выбранного на этом шаге, обозначим через . В рассматриваемой задаче пошаговой оптимизации целевая функция (2) полагается аддитивной, т. е.

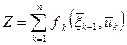(3)

Обычно условиями процесса на управление на каждом шаге накладываются некоторые ограничения. Управления, удовлетворяющие этим ограниче­ниям, называются допустимыми.

Задачу пошаговой оптимизации можно сформулировать следующим образом. Определить совокупность допустимых управлений переводящих систему из начального состояния в конечное состояние и максимизирующих или минимизирующих показатель эффективности (3). В дальнейшем будем рассматривать задачу на максимум.

Начальное состояние и конечное состояние могут быть заданы однозначно или могут быть указаны множество начальных состояний и множество конечных состояний так, что 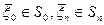. В последнем случае в задаче пошаговой оптимизации требуется определить совокуп­ность допустимых управлений, переводящих систему из начального состоя­ния в конечное состояние 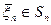и максимизирующих целевую функцию (3). Управление, при котором достигается максимум целевой функции (3), называется оптимальным управлением и обозначается через .

Поиск по сайту: