Оптимизация на графах

Основные понятия теории графов

Наука, занимающаяся графическими представления­ми,- геометрия из-за своей наглядности получила широ­кое распространение уже в древности. Так, задолго до жив­шего в VI в. до н. э. Пифагора была известна теорема, ко­торая позже стала носить его имя. Наглядность геометрии широко используют в наше время, в том числе при анализе больших технических и организационных систем, в кото­рых используют теорию графов.

Граф - совокупность вершин и ребер - универсаль­ное средство наглядного представления достаточно разно­образных задач (рис. 9а).

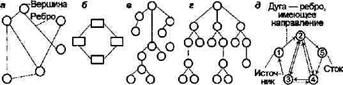Рис. 9

Разнообразные сочетания различных ребер и вершин пред­ставляют многообразие возможных графов и их применения. Граф, в котором вершины - прямоугольники и направле­ния ребер не заданы, описывает блок-схему (или структу­ру) технической системы (рис. 9б). Рисунок 9в - граф-дерево (например, описание метода ветвей и границ) - много­уровневая иерархическая система, в которой все вершины распределены по нескольким уровням.

Граф 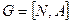это совокупность двух множеств: 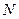- множество некоторых элементов 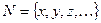, называемых вершинами, 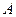- множество некоторых упорядоченных пар элементов множества 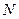, вершины 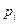и 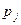называются концевыми точками или концами ребра 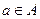. Граф называется конечным, если множества 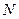и 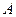конечны.

Это определение графа должно быть дополнено в одном важном отно­шении. В определении ребра можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок несуществе­нен, т. е. если 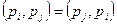,то говорят, что а есть неориентированное ребро; если же этот порядок существенен, то а называется ориентированным ребром (ориентированное ребро часто называется дугой). В последнем случае 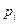называется также начальной вершиной, а 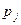- конечной верши­ной ребра а. Граф называется неориентированным, если каждое его ребро неориентировано, и ориентированным, если ориентированы все его ребра. В ряде случаев естественно рассматривать смешанные графы, имеющие как ориентированные, так и неориентированные ребра.

Ребра, имеющие одинаковые концевые вершины, называются параллельными. Ребро, концевые вершины которого совпадают, называется пет­лей. Она обычно считается неориентированной. Вершина и ребро называют­ся инцидентными друг другу, если вершина является для этого ребра конце­вой. Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль - графом. Две вершины, являющиеся концевыми для некоторого ребра назы­ваются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными.

Число ребер, инцидентных одной вершине 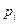, будем обозначать че­рез 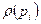. Это число называется локальной степенью или просто степенью графа в вершине 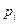. В случае ориентированного графа G обозначим через 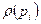и 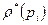число ребер, соответственно выходящих из вершины 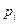и входящих в 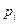. Эти числа называются локальными степенями G 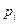. Если все числа 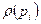конечны, то граф называется локально-конечным. Вершина степени 1 называется висячей. Вершина степени 0 называется изолиро­ванной.

Теорема 1. В графе G сумма степеней всех его вершин - число п четное, равное удвоенному числу ребер графа: 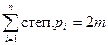, где п - число вершин графа, m - число его ребер.

Теорема 2. Число нечетных вершин любого графа, т.е. вершин, имеющих нечетную степень, четно.

Граф G называется полным, если любые две его различные вершины соединены ребром, и он не содержит параллельных ребер. Дополнением графа G называется граф 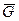с теми же вершинами, что и граф G и содержа­щий только те ребра, которые нужно добавить к графу G чтобы получился полный граф. Граф G называется плоским, если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами.

Рисунок 9д - граф с дугами, изображающими связь между вершинами, - сеть.

Сетями представляют различные задачи, в которых ис­следуют перемещение или выполнение работ во времени. Сеть характеризуется структурой и параметрами дуг. Струк­тура (топология) сети показывает, какие вершины связаны между собой, и направление связывающих их дуг.

Каждую вершину сети нумеруют порядковым номе­ром. Начальную 1 вершину в описании движения потоков называют источником, конечную - стоком.

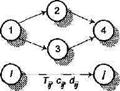
Рис. 10

Дугу (рис. 10) обозначают двойной индексацией 1-2; 3-4 и т.д. В общем случае дугу обозначают i-j, где i - номер вершины, из которой исходит дуга; j - номер вершины, в которую входит дуга. Каждая дуга имеет свою характеристику: t_ij - продолжитель­ность движения по дуге i-j; c_ij - стоимость перемещения; d_ij - пропускная способность дуги и т.д.

Зная топологию сети и ее параметры, можно решать самые разнообразные, часто встречающиеся задачи опти­мизации.

Поиск по сайту: