АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Классификация и общая постановка задач нелинейного программирования

Читайте также:
  1. Data Mining и Business Intelligence. Многомерные представления Data Mining. Data Mining: общая классификация. Функциональные возможности Data Mining.
  2. FECONCL (ББ. Экономическая классификация)
  3. I Классификация кривых второго порядка
  4. I Психологические принципы, задачи и функции социальной работы
  5. I. 1.1. Пример разработки модели задачи технического контроля
  6. I. 1.2. Общая постановка задачи линейного программирования
  7. I. 2.1. Графический метод решения задачи ЛП
  8. I. 3.1. Двойственная задача линейного программирования
  9. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  10. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  11. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  12. I. Общая установка сознания

Задачи нелинейного программирования - большой класс разнообразных задач, из которых будем рассматривать только сводящиеся к задачам линейного программирования.

Ранее в задачах линейного программирования полага­лось, что себестоимость, цена и другие показатели эффек­тивности на единицу продукции не зависят от изменения объема производства. Однако в общем случае зависимости между переменными в ограничениях и целевой функции не могут быть линейными. Например, себестоимость единицы продукции снижается при увеличении объема производства.

Задачи, в которых зависимости между переменными в целевой функции и/или в ограничениях нелинейны, назы­вают задачами нелинейного программирования.

Если обозначить целевую функцию и ограничения че­рез обобщенную функцию h(хj), то все многообразие задач нелинейного программирования можно свести к классифи­кации (см. табл. 16).

В общем виде задача НЛП состоит в определении мак­симума (минимума) функции

(1)

при условии, что ее переменные удовлетворяют условиям

(2)

где f и gi - некоторые известные функции п переменных; bi - заданные числа.

Таблица 16

Отрезок, соединяющий две точки Вид функции Число оптимумов График
Совпадает   Линейная  
Выше вершины >0 Выпуклая вниз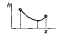  
Ниже вершины <0 Выпуклая вверх (вогнутая вниз)  
По обе стороны от вершины Меняет знак Смешанная Несколько

 

Здесь имеется в виду, что в результате решения задачи будет определена точка координаты которой удовлетворяют соотношениям (2), и такая, что для всякой другой точки удовлетворяющей условиям (2), выполняется неравенство

при max целевой функции или

при min целевой функции.

Если f и gi - линейные функции, то задача (1), (2) - задача линейного программирования.

Соотношения (2) образуют систему ограничений и вклю­чают условия неотрицательности переменных, если такие имеются. Условия неотрицательности переменных могут быть заданы и непосредственно.

Нелинейные задачи решаются с помощью метода кусочно-линейной аппроксимации или метода множителей Лагранжа, В задачах квадратичного программирования применяется ме­тод Била, Баранкина-Дорфмана, градиентные методы (метод Франка-Вулфа, штрафных функций, метод возможных на­правлений). В градиентных методах итерационный процесс осуществляется до того момента, пока градиент функции f(x) в очередной точке xk+1 не станет равным нулю или пока 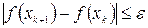(достаточно малое положительное число, ха­рактеризующее точность полученного решения).

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)