Задача о кратчайшем пути

Частным случаем задачи об оптимальном потоке является задача по­строения кратчайшего пути между двумя вершинами пути. Пусть дан граф G=[N, A], каждой дуге которого поставлено в соответствие чис­ло С(х, у), называемое длиной дуги (х, у). Выделяются две вершины гра­фа - s и t. Требуется найти путь наименьшей длины, ведущий из вершины s в вершину t. При этом длина произвольного пути определяется следующим образом:

.

Данная задача может быть сформулирована как задача об оптимальном пото­ке. Ставится задача определения потока, минимизирующего функционал

, где .

Рассмотрим теперь сеть, вершина s которой является источником еди­ничной интенсивности, t - стоком единичной интенсивности, остальные вершины - нейтральные. Дугам приписываются неограниченные пропускные способности, а стоимость перевозок по дуге полагается равной длине дуги. Для потока в рассматриваемой сети

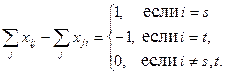
Пусть имеется некоторый конечный граф G = [N ={1,2,…,n}, а], каж­дой вершине i которого поставлено в соответствие некоторое число , назы­ваемое интенсивностью потока. Вершины назовем источниками, нейтраль­ными вершинами и стоками, если , и 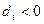соответственно. По­током в полученной сети назовем совокупность величин , удов­летворяющих соотношениям

,

.

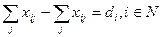Поиск по сайту: