 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Динамическое программирование. Оптимизация с дискретным временем
Оптимизация с дискретным временем
Система наблюдается в моментах времени t=0,1,…,T.
Состояние системы характеризуется числом xt ÎR. Известно значение x0. Система меняет своё состояние под воздействием управлений ut, которые можно свободно выбирать из заданного множества U, которое назовём областью управления. Управления влияют на состояния системы по правилу
xt+1=g(t,xt,ut),
utÎU, (1)
где g – заданная функция.
Предположим, что выбраны величины u0,u1,…,uT-1. Тогда, начиная с x1=g(0,x0,u0), получим x2=g(1,x1,u1) ит.д.
Таким образом, каждому выбору управлений соответствует свой путь (или график).
Пусть имеется функция f(t,x,u) такая, что польза от выбранного пути есть сумма:
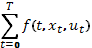 (*) Эта сумма носит название целевой функции.
(*) Эта сумма носит название целевой функции.
Иногда вместо 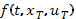 рассматривают
рассматривают 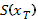 .
.
Вместе с заданной последовательностью 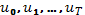 находим последовательность
находим последовательность 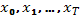 и получаем допустимую пару. При этом целевая функция принимает определенное значение.
и получаем допустимую пару. При этом целевая функция принимает определенное значение.
Задача состоит в том, чтобы среди всех допустимых пар 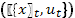 найти оптимальную пару
найти оптимальную пару 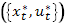 , дающую наибольшее значение целевой функции.
, дающую наибольшее значение целевой функции.
Задача, в краткой формулировке, записывается так:
найти 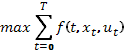 при условиях
при условиях 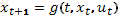 ,
,  задано,
задано, 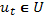 (2)
(2)
Поиск по сайту: