 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Рассмотрим задачу найти
 ,
,
 , t=0,…,T-1 (1)
, t=0,…,T-1 (1)
 – задано,
– задано,  – свободно
– свободно
Пусть U представляет собой интервал
Определим функцию Понтрягина (Hamiltonian)
 (2)
(2)
 – сопряжения (присоединения) функции
– сопряжения (присоединения) функции
Теорема (принцип максимума необходимое условие).
 - пара оптимальных последовательностей уравнения (1) и H определено в (2)
- пара оптимальных последовательностей уравнения (1) и H определено в (2)
Тогда существуют  , с условием
, с условием  такие, что для всех t=0,…,T-1:
такие, что для всех t=0,…,T-1:
 (3)
(3)

Если  - внутри U, тогда:
- внутри U, тогда:
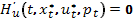
Кроме того,  удовлетворяет разностному уравнению:
удовлетворяет разностному уравнению:
 , t=0,…,T (4)
, t=0,…,T (4)
Теорема (достаточное условие).
Если выполнены условия Теоремы 1 и H(t,x,u,p) выпукла вверх по x,uдля любого t, тогда тройка  - оптимальна.
- оптимальна.
Пример



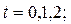

При t <3 функция Понтрягина равна:

При t =3 функция Понтрягина:

Функция Понтрягина выпукла вверх по (x; u). Область управления U открытая => (3) => 

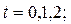

 =>
=> 


Разностное уравнение (4) для pt имеет вид:

 и, следовательно,
и, следовательно,

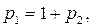
 так как x3 свободен,
так как x3 свободен,  таким образом,
таким образом,


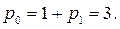
Поэтому оптимальное управление:



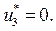
Поиск по сайту: