 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примечание. Теорема справедлива и в том случае, когда область управления не фиксирована, но зависит от и ,
|
Читайте также: |
Теорема справедлива и в том случае, когда область управления не фиксирована, но зависит от 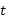 и
и 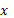 ,
, 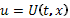 . Тогда максимизация в (2), (3), (5) выполняется при
. Тогда максимизация в (2), (3), (5) выполняется при 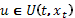 . В (6)(стр. 7),(7)(стр. 7) максимизациявыполняется при
. В (6)(стр. 7),(7)(стр. 7) максимизациявыполняется при 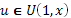 и
и 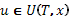 , соответственно.
, соответственно.
Часть множеств 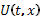 задается набором неравенств
задается набором неравенств 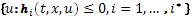 .
.
Если 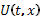 - пустое множество, то принимается соглашение, по которому максимум взят по этому множеству равен -
- пустое множество, то принимается соглашение, по которому максимум взят по этому множеству равен -  .
.
Рассмотрим задачу, в которой
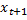 =
= 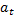 (
(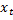 -
- 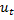 ),
), 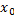 > 0,
> 0, 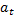 - заданные положительные числа
- заданные положительные числа
β = 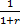 , r – уровень дисконтирования, 0 <
, r – уровень дисконтирования, 0 < 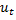 <
< 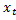 , γ
, γ 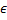 (0, 1), A>0
(0, 1), A>0
Ищется
max ( +
+  ) (I)
) (I)
В соответствии со сделанным замечанием, 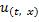 = (0, x)
= (0, x)
f(t, x, u) = 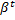
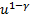 , t = 0, 1, … T-1
, t = 0, 1, … T-1
f(T, x, u) =  - эта функция от u не зависит, и ее максимум, равный
- эта функция от u не зависит, и ее максимум, равный 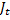 совпадает с ней самой,
совпадает с ней самой, 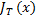 =
=  (II), и любое
(II), и любое 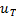 = (0, x) – оптимальное.
= (0, x) – оптимальное.
Из (6) получаем
 =
= 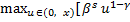 +
+  (x-u))] (III)
(x-u))] (III)
При s = T-1
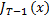 =
= 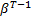
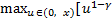 +
+ 
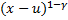 ] (IV),
] (IV),
так как
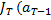 (x-u)) =
(x-u)) = 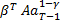
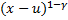
Для 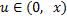 обозначим
обозначим
g(u) = 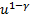 +
+ 
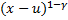
Тогда g’(u) = (1-γ)  + (1-γ)(-1)
+ (1-γ)(-1) 
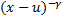
g’(u) =0 ó  = (-1)
= (-1) 
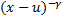
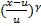 =
= 
 = 1 +
= 1 + 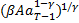 =
= 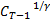 (V)
(V)
u = 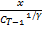
так как g’(u) = (1-γ)(-γ)  + (1-γ)(-γ)
+ (1-γ)(-γ) 
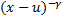 ,
, 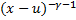 < 0,
< 0,
поэтому 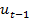 максимизирует g(u)
максимизирует g(u)
g (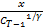 ) =
) = 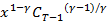 + β A
+ β A  =
=
= 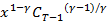 +
+  =
= 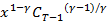 (1 + β A
(1 + β A  (
(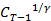 -1)) =
-1)) =
β A  =
= 
= 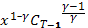 (1 +
(1 +  -1) =
-1) = 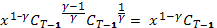 (VI)
(VI)
Тогда ввиду (IV), (VI) (в (VI) вычитаем max y(u), подставляем в (IV))
 (x) =
(x) = 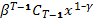
Отметим, что 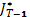 имеет тот же вид, что и
имеет тот же вид, что и 
Для s= T-2
 (x) =
(x) = 
По аналогии со сделанным выше находим, что максимум достигается при  = u =
= u = 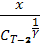 , где
, где 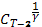 = 1+
= 1+ 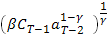 и где
и где  (x) =
(x) = 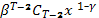
Продолжая аналогично, находим для любого t
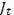 (x) =
(x) = 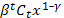 , где
, где 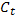 = A, а для
= A, а для 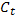 при t<T имеем
при t<T имеем
 = 1+
= 1+ 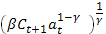 = 1 +
= 1 + 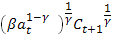
Оптимальное управление:
 (x) =
(x) = 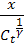 , t<T
, t<T
Для нахождения оптимальных 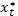 подставляем эти значения в рекурсивное уравнение
подставляем эти значения в рекурсивное уравнение

Предположим что для всех t тогда
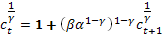
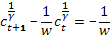
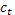 линейное уравнение первого порядка с постоянным коэффициентом
линейное уравнение первого порядка с постоянным коэффициентом
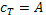
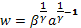
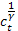 =
= 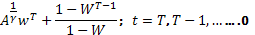
См раздел 14 страница 1 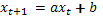
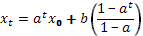
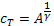
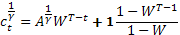
Поиск по сайту: