 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Infinite Horizon
|
Читайте также: |
Неограниченный период.
Проблема ставится так:
найти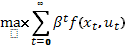 
(1)
при условии, что 
- заданное число,
…
.
, 
– допустимая пара последовательностей, если - задано, 
, 
определяется уравнением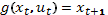 
. При этом 
, g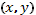 
не зависят от переменной t явно. Таким образом (1) называется автономным рядом.
f удовлетворяет условиям ограниченности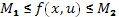 
для всех x,u, u 
. Поэтому ряд в (1) сходится. Сравним с прогрессией.
Пусть π̅ = (us, us+1, …) – последовательность управлений, гдеus+kϵU, k = 0, 1, …;xt+1 = g(xt, ut), t = s, s+1, …; xs = x.
Тогда польза, полученная за период t = s, s+1, … равна
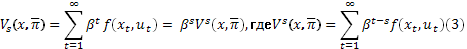
Положим, что
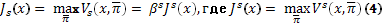
и максимумы взяты по всем последовательностям π̅.
Таким образом, 
– максимальный успех, который можно получить от t=s до +∞.
При условии, что в момент t=s система находится в состоянии x, называется оптимальной целевой функцией для задачи (1).
Имеем 
Максимизируя 
получаем одно и то же значение в обоих случаях, поскольку будущее (+∞) выглядит вполне одинаково в момент 0 и в момент s.
Из (5) следует: 
Положим, по определению 
Из (6) следует, что если мы знаем 
, то мы знаем для всех s.
Теорема. Целевая функция в (4) для задачи (1) удовлетворяет уравнению Беллмана.
J (x) = max [f(x,u)+ßJ(g(x,u))] (8)
uÎU
Грубое рассуждение напоминает рассуждения для конечного периода Т. Предположим, что мы при t=0 находимся в состоянии х. Выбрав управление u, получаем βо f(x,u)=f(x,u) и во время t=1 попадаем в x1=g(x,u).
Выбор оптимальной последовательности управлений при t=1 и так далее даёт прибавку в последующий период J1(g(x,u))=βJ(g(x,u)). Следовательно, наилучший выбор при t=0, тот что максимизирует сумму f(x,u) +βJ(g(x,u)), поэтому максимум этой суммы равен J(x)
(8) – функциональное уравнение, можно доказать, что при условиях ограниченности (2), и полагая, что максимум в правой части (8) существует, это уравнение имеет единственное решение которое автоматически является оптимальным уравнением u(x), максимизирующее правую часть (8) — оптимальное и оно не зависит от t. Обычно решить уравнение (8) бывает непросто.
Поиск по сайту: