Свойства целевой функции

Пусть при система имеет значение x. Наилучшее, что можно сделать в оставшийся период – выбрать (следовательно, ) так, чтобы максимизировать при .

Назовем оптимальной целевой функцией для этой задачи в момент s.

(3)

где , , , (4)

Управления, максимизирующие (3) при условиях (4), зависят от х. В частности, зависит от х.

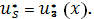Управления, зависящие от состояния системы назовем политиками.

Если мы напишем для каждого политику, то мы тем самым решили задачу (2)

Рассмотрим важное свойство целевой функции. При 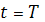имеем

.

Пусть при система в состоянии . При выборе при получен выигрыш , при этом система окажется в состоянии

При этом наибольший полный выигрыш, который можно получить от до , начиная с состояния , равен

Следовательно, наилучшим выбором для будет то, которое максимизирует сумму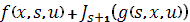

Теорема: Пусть обозначает целевую функцию в момент

, ,

для задачи найти:

(5)

при условиях , – задано,

Тогда удовлетворяет уравнениям

(6)

(7)

Замечание: Разумеется значения выбираются среди решений разностного уравнения (1) при фиксированном и возможных выборах .

Обычно эта теорема используется так: ищем функцию (7).

Максимизируются значение U*_T (x). Следующий шаг – используя (6) найти J_T-1(x) и соответствующую W*_T-1(x). Действуя аналогично, находим все J_T (x), J_T-1(x),….,J₀(x) и соответствующие U*_T(x), U*_T-1(x),…,U*₀(x).

Это позволяет построить решение исходной задачи оптимизации.

Пример.

Рассмотрим задачу найти:

max 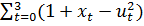, при условиях , t=0, 1, 2, , .

Здесь T=3, f(t,x,u)=1+x-u², g(t,x,u)=x+u.

Из (7) при T=3получаем, что J₃(x) представляет собой наибольшее значение функции , .

Оно получается при u=0, т.е. J₃(x)=1+x, .

При s=2 функция максимизируется, обозначим ее h₂(u)=1+x-u²+J₃(x+u)

Так как J₃(x)=1+x, J₃(x+u)=1+(x+u) и h₂(u)=1+x-u²+1+x+u=2+2x+u-u²; h₂’(u)=1-2u, h₂’(u)=0, u=1/2, h₂(u) выпукла вверх, то u, u₂*(x)=1/2, J₂(x)=h₂(u₂*(x))=2+2x+1/2-1/4=2x+9/4.

При s=1 мы максимизирует функцию h₁(u)=1+x-u²+2(x+u)+9/4=3x+2u-u²+13/4

h₁’(u)=2-2u; h₁’(u)=0, u=1.

Находим u₁*(x)=1 и J₁(x)=3x+2-1+13/4=3x+17/4.

При s=0 максимизируется функция

.

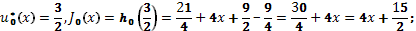
Укажем оптимальные значения состояния системы:

Оптимальное значение целевой функции:

.

В простых случаях, подобных рассмотренному, задача динамической оптимизации допускает решение с использованием обычных методов анализа.

Полагая в уравнении

последовательно получаем

Таким образом, максимизация целевой функции равна

- матрица 2 дифференциала

По критерию Сильвестра второй дифференциал – отрицательно определенная форма следовательно получаем тоже максимум

Подобный подход возможен в любой задаче, но он слабо реализуем при больших T.

Рассмотрим еще одну задачу:

Найти

max

при условии

Поскольку и
для t выполняется неравенство

Далее, независимо от u, и поэтому и любое решение оптимальнее

Уравнение (1) при S=T-1 дает

Первая производная по u функции равна

,

1+ux=3/2, ux=1/2.

При этом .

Итак, ()

Рассмотрим уравнение (6) при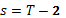

Снова получаем

,

при этом

Очевидно, что далее, продолжая процесс, получим

Подстановка в разностное уравнение дает =

При этом .

Поиск по сайту: