АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение Эйлера. Рассмотри задачу найти (1) при заданном значении и свободно изменяющихся

Читайте также:
  1. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  2. IV. УРАВНЕНИЕ ГАМЛЕТА
  3. V2: Волны. Уравнение волны
  4. V2: Уравнение Шредингера
  5. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  6. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  7. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  8. В простом случае обычное дифференциальное уравнение имеет вид
  9. В этом случае уравнение Эйлера принимает вид
  10. ВКЛАД Эйлера в РАЗВИТИЕ тригонометрии
  11. Влияние температуры на константу равновесия. Уравнение изобары
  12. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона

Рассмотри задачу найти (1) при заданном значении и свободно изменяющихся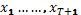

С другой стороны часто можно переформулировать задачу динамического программирования в виде (1)

Если положить получим задачу с U=R

 

Предположим что уравнение при любом выборе и имеет единственное решение U

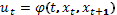
Определим f()=f(t, xt, )= при

t<T и .

Иными словами,

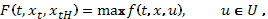
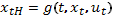
Пусть , …, - оптимальное решение задачи (1). Для любого заданного t производная выражения (1) по равна 0. Положим , тогда , …, удовлетворяют уравнению Эйлера:

(2)

номер переменной функции F, по которой взята производная
t=0,1,…,T

 

Это разностное уравнение второго порядка, подобное уравнению Эйлера из вариационного исчисления.

При t = T уравнение (2) переходит в , из которого находим

Эта величина подставляется в (2) при t = T-1 и получаем и т.д., так не получим , а задано


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)