АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача. На множест­ве решений системы неравенств

Читайте также:
  1. В) Задача.
  2. В) Задача.
  3. Задача.
  4. Задача.
  5. Задача.
  6. Задача.
  7. Задача.
  8. Задача.
  9. Задача.
  10. Задача.
  11. Задача.

На множест­ве решений системы неравенств

+ ≤ 36;

найти глобальные экстремумы функции .

Решение. На рис. 1 множество допустимых реше­ний заштриховано. Это мно­жество выпукло. Линиями уров­ня функции z = 2х + у являют­ся параллельные прямые с уг­ловым коэффициентом К = - 2. Очевидно, что глобальный ми­нимум достигается в точке О(0; 0), а глобальный макси­мум— в точке А касания пря­мой уровня и окружности х2 ± y2 = 36. Найдем координа­ты точки А. Для этого доста­точно составить уравнение пря­мой l и решить систему, со­стоящую из уравнения прямой и уравнения окружности. За­метим, что прямая l перпенди­кулярна линии уровня, а, следо­вательно, ее угловой коэффици­ент К1 равен (К1К = — 1). Прямая l проходит через точку Ои имеет угловой коэффициент

К 1 = .

 

 

 

Рис. 1

Поэтому ее уравнение таково : у = .

Решая систему

+ = 36;

у = ,

получаем

Итак, глобальный минимум, равный 0, достигается в точке О (0;0), а глобальный максимум, равный 6 , — в точке А (2,4- 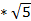; 1,2* ). Локальных экстремумов, отличных от глобальных, функция не достигает.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)