АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Матрицы

Читайте также:
  1. I. Определение ранга матрицы
  2. II. Умножение матрицы на число
  3. II. Элементарные преобразования. Эквивалентные матрицы.
  4. SWOT- анализ и составление матрицы.
  5. Алгоритм вычисления обратной матрицы.
  6. Алгоритм вычисления обратной матрицы.
  7. Алгоритм Гаусса вычисления ранга матрицы
  8. Алгоритм нахождения обратной матрицы
  9. Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.
  10. Б) с помощью обратной матрицы.
  11. Базисный минор и ранг матрицы. Теорема о базисном миноре
  12. Билет 21 Квадратичные формы, преобразование матрицы квадратичной формы при переходе к новому базису.

 

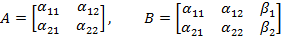
называется соответственной основной и расширенной матрицами системы (1). Чтобы исключить неизвестное 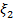, умножим первое из уравнений на 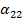, второе на 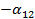и сложим их. В результате получим уравнение

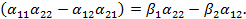
Если 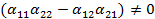, то из этого уравнения и аналогичного уравнения, получающегося путем исключения 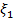, получим

 

 

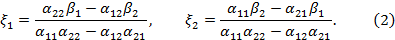
Знаменатели выражений для неизвестных здесь одинаковы и представляют собой многочлен от элементов основной матрицы А. Значение этого многочлена называют определителем или детерминантом матрицы А и обозначают или .

Если матрица задана своей таблицей, то детерминант обозначают, заключая таблицу в вертикальные черты. Таким образом, по определению для любой квадратной матрицы 2-го порядка

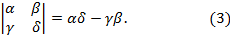
С помощью определителей формулы (2) можно переписать в виде

 

 

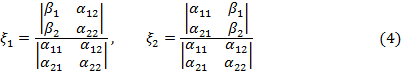
Решая аналогичным путем систему трех уравнений

 

(5)

 

с тремя неизвестными 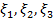, получим

 

 

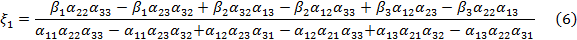
и аналогичные выражения для . Конечно, эти выражения имеют смысл лишь в том случае, когда знаменатель их отличен от нуля.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)