АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача. Определить наибольшее значение функцииz = при условии

Читайте также:
  1. В) Задача.
  2. В) Задача.
  3. Задача.
  4. Задача.
  5. Задача.
  6. Задача.
  7. Задача.
  8. Задача.
  9. Задача.
  10. Задача.
  11. Задача.

Определить наибольшее значение функцииz = 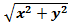при условии

 

Решение. Множество до­пустимых решений заштрихова­но на рис. 2. Если целе­вой функции придавать фикси­рованные значения с, то будем получать окружности с центром в начале координат и радиусом с2. Пусть с = 1, 2,... Начертим ряд окружностей (линии уров­ня целевой функции). Из рисунка 2 видно, что функция z = 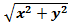достигает наиболь­шего значения, равного 8, в точ­ке A (8;0): z = 8.

 

 

Рис.2

К рассматриваемому типу нелинейных задач относятся и за­дачи с дробно-линейной целевой функцией.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (2.679 сек.)