Пример. Найти минимальное значение целевой функции

на множестве решений системы

Решение. Здесь - свободные переменные. Перепишем систему ограничений (1) в виде

Исходным базисным решением является решение (7; 0; 0; 12; 0; 10), при котором значение функции равно нулю. Целевая функция уже выражена через небазисные переменные. Значение целевой функции может быть уменьшено за счет увеличения . Среди коэффициентов при в системе (2) имеются отрицательные: и . Находим отношения (из второго уравнения системы (2)): . Элемент – разрешающий. Из старого базиса исключим и введем в него из небазисных переменных . Для этого выразим через и из второго уравнения и найденное выражение подставим вместо в первое и третье уравнения системы (2), а также в выражение F.

Получим систему (3), где 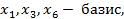- свободные переменные.

Min

Новое базисное решение имеет вид: (10; 0; 3; 0; 0; 1). . Значение F можно уменьшить за счет увеличения . Среди коэффициентов при в системе (3) только один отрицательный: Элемент разрещающий. Перейдем к новому базису: (своб.:

Новое базисное решение имеет вид: , Дальнейшее уменьшение значения целевой функции невозможно.

Практическое решение задач линейного программирования, как правило, обычно проводится так: коэффициенты при переменных переписываются в специальные таблицы – симплексные таблицы (собственно мы это уже сделали при нахождении базисных решений системы линейных уравнений).

Поиск по сайту: