Градиентный метод нелинейного программирования

Пусть мы имеем некоторую функцию двух действительных переменных и некоторую точку A , принадлежащую области определения X этой функции. Назовем градиентом функции f вектор (символ читается: «набла» ).

Градиент в точке А перпендикулярен касательной к линии уровня функции

в этой точке. Например дана функция . Построим несколько ее линий уровня (рис. 55):

Известно, что направление градиента служит направлением максимальной скорости роста функции. На примере задачи с двумя переменными покажем геометрическую картину градиентного метода.

Рис 55.

Задача 7.6.1. Найти глобальный максимум на множестве решений системы неравенств.

Предположим, что мы начинали с некоторого допустимого решения, определённого координатами точки . Градиент или является вектором, перпендикулярным касательной к линии уровня в точке . Мы двигаемся из точки в направлении до тех пор, пока не достигнем границы множества допустимых решений . Дальше мы не можем двигаться в направлении , так как при этом мы выйдем из множества допустимых решений. Поэтому мы выбираем вектор , составляющий с вектором наименьший угол по сравнению с любым другим вектором с началом в точке и лежащим в множестве допустимых решений. Таким образом, на следующем шаге мы двигаемся вдоль прямой Это приводит нас в точку На этом процесс заканчивается. Геометрически это выражается тем, что составляет тупой угол с любым вектором в множестве допустимых решений, выходящим из точки А. Заметим что в точке 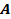функция достигает глобального максимума: Предположим теперь, что, решая эту же задачу, в качестве начального допустимого решения мы выберем точку (рис. 56). В этом случае мы сначала по направлению 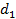достигаем точки , а затем по направлению вдоль прямой попадаем в точку . На этом процесс заканчивается: В точке функция достигает лишь локального максимума. Даже на одном примере видно, что результат решения зависит от того, с какой точки допустимого решения начинается процесс.

Рис. 56.

Градиентные методы в лучшем случае обычно сходятся лишь к локальному минимуму. Впрочем бывает и так, что даже такая сходимость отсутствует.

Только в том случае, когда задача обладает подходящими свойствами выпуклости или вогнутости, можно быть уверенным, что процесс сходиться к глобальному экстремуму.

Рассмотрим далее идею метода обхода узлов пространственной сетки. Он заключается в том, что для каждой переменной устанавливается определенный интервал изменения (шаг поиска). Затем берем начальную точку с минимальными координатами и проверяем, входит ли эта точка в множество допустимых решений. После этого вычисляем в ней значение целевой функции. Увеличиваем одну из координат на заданный интервал, а остальные координаты оставляем без изменения. Таким образом осуществляется передвижение вдоль одной оси на величину шага. Для новой точки тоже проверяем ее принадлежность множеству Ω и вычисляем значение целевой функции. Опять увеличиваем на интервал ту же координату и испытываем полученную точку и т.д. Дойдя до границы множества Ω, изменяем на величину шага другую координату, т. е. смещаемся в сторону, и снова от некоторой начальной точки двигаемся до границы области и т.д. (рис. 57). Здесь значениям переменных

геометрически соответствуют параллельные гиперплоскости, отстоящие друг от друга на величину шага . Число систем таких плоскостей равно числу переменных. В пересечениях они образуют точки - узлы пространственной сетки. В процессе поиска мы обходим поочередно узлы, принадлежащие многограннику допустимых планов, и вычисляем в каждом случае значение целевой функции. Наибольшее (наименьшее) из них указывает с точностью до шага оптимальную точку. Этот метод, как нетрудно было уже заметить, связан с ог­ромным объемом вычислительной работы. Он пригоден для ре­шения задач с малым числом переменных и с обязательным применением электронных вычислительных машин.