Метод искусственного базиса

Если основная задача ЛП не является канонической или почти канонической, то симплексным методом можно провести исследование линейной системы основной задачи, что позволит:

1) Установить наличие или отсутствие планов у данной системы

2) В случае существования планов построить каноническую систему, равносильную исходной. Две системы с одним и тем же числом неизвестных равносильны (эквивалентны), если каждое решение первой системы является в то же время решением второй системы и наоборот [2].

Рассмотрим пример исследования линейной системы симплексным методом:

(*)

Система неканоническая (нет базиса). Введем искусственный базис с помощью так называемых фиктивных переменных , . Полученная система является канонической:

1. Для того чтобы линейная система (*) обладала планами, необходимо и достаточно, что бы минимальное значение целевой функции вспомогательной (**)

задачи было равно нулю 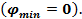Если же , то линейная система заведомо планов не имеет [4].

Решим сформулированную вспомогательную задачу: при условиях (**). В задаче минимизации нас интересуют положительные оценки.

Исходная таблица

B		Коэффициенты при неизвестных

 

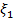
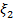
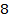
Итерация 1

B		Коэффициенты при неизвестных

 

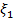
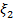
					Итерация 2
B		Коэффициенты при неизвестных

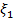
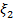
Оптимальное решение вспомогательной задачи достигнуто.

(32/5; 0; 2/5; 0; 0;) .

Следовательно, линейная система (*) совместна.

2. Если линейная система уравнений обладает планами, то существует равносильная ей каноническая система, которую можно получить из завершающей симплексной таблицы вспомогательной задачи [4].

Таблица «Итерация 2» содержит каноническую систему

Из этой канонической системы при получаем каноническую систему, равносильную исходной (*):

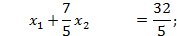
Среди базисных переменных последней симплексной таблицы «Итерация 2» нет ни одной фиктивной переменной.

3. Далее решаем каноническую (или почти каноническую) задачу ЛП: минимизировать (максимизировать) целевую функцию F основной задачи ЛП при условиях (***).

Однако может быть случай, когда среди базисных переменных последней симплексной таблицы есть хотя бы одно фиктивное. В этом случае из данной таблицы нельзя сразу выделить каноническую систему. К ней приходят после некоторых преобразований.

4. И, наконец, может быть случай, когда , то есть исходная система планов не имеет и равносильной ей канонической системы не существует [4]. Например:

Исходная таблица

B		Коэффициенты при неизвестных

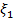
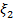
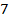
Итерация 1

B		Коэффициенты при неизвестных

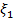
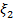
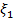
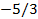
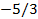
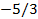
Так как , то исходная система планов не имеет (равносильной ей канонической системы не существует).

Поиск по сайту: