АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Необходимые и достаточные условия условного экстремума. Принцип Лагранжа

Читайте также:
  1. A) подписать коллективный договор на согласованных условиях с одновременным составлением протокола разногласий
  2. B. Основные принципы исследования истории этических учений
  3. ERP-стандарты и Стандарты Качества как инструменты реализации принципа «Непрерывного улучшения»
  4. I Психологические принципы, задачи и функции социальной работы
  5. I Распад аустенита в изотермических условиях
  6. I. МЕСТО И ВРЕМЯ КАК ГРАНИЧНЫЕ УСЛОВИЯ
  7. I. Неблагоприятные условия для жизни бактерий создаются при
  8. I. Необходимые документы для участия в Конкурсе
  9. I. Правила поведения в условиях вынужденного автономного существования.
  10. I. При каких условиях эта психологическая информация может стать психодиагностической?
  11. I. Психологические условия эффективности боевой подготовки.
  12. I. Сестринский процесс при гипертонической болезни: определение, этиология, клиника. Принципы лечения и уход за пациентами, профилактика.

В задачах условной оптимизации область допустимых решений содержит ограничения на вектор х:

при ограничениях

Рассмотрим задачу условной оптимизации при ограничениях типа неравенств:

при ограничениях

,

где целевая функция f(x) = f (x1,x2,...,xn) и функции ограничений gi (x1,x2,…xn) непрерывно дифференцируемые функции.

Необходимое условие экстремума для задачи (2.3) формулируется в виде принципа Лагранжа.

Принцип Лагранжа. Пусть х* - точка локального экстремума функции f(x), причем векторы линейно независимы. Тогда найдутся такие числа 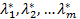, не равные одновременно нулю, что для функции Лагранжа

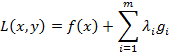
выполняются следующие равенства:

 

Числа называются множителями Лагранжа. Система (2.4) содержит n + m уравнений с n + m неизвестными . Точки х* = (х1*, х2*, …, хn*), удовлетворяющие условиям (2.2) при некоторых , называются условно-стационарными. Тип условно-стационарной точки х* определяется знаком второго дифференциала функции Лагранжа (необходимым условием второго порядка):

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)