Вырожденная задача ЛП

При рассмотрении симплексного метода предполагалось, что все 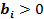как в исходной системе, так и в системах, получаемых после определенных итераций. Если же в некоторых уравнениях, , то возникает неоднозначность в выборе решающего элемента и в соответствующем базисном решении. Базисные переменные, относительно которых эти уравнения разрешены, принимают нулевые значения. Базисное решение, в котором хотя бы одна из базисных переменных равна нулю, называется вырожденным решением, а задача ЛП, имеющая хотя бы одно вырожденное решение, называется вырожденной задачей.Применяя (в случае вырожденной задачи) последовательные итерации, мы можем вернуться к ранее встречавшемуся базисному решению, т.е. появляется так называемое зацикливание (значение линейной формы не меняются от итерации к итерации) в схеме расчета.

Если на каком либо этапе расчета возникает неопределенность в выборе разрешающей строки, т.е. окажется несколько равных минимальных отношений , то следует выбирать ту строку, для которой отношение элементов следующего столбца к разрешающему будет наименьшим. Если при этом снова окажутся равные минимальные отношения, то составляются отношения элементов следующего столбца, и так до тех пор, пока разрешающая строка не определиться однозначно.

Поиск по сайту: