АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Геометрическая интерпретация и графический способ решения задачи квадратичного программирования

Читайте также:
  1. FAST (Методика быстрого анализа решения)
  2. I Психологические принципы, задачи и функции социальной работы
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. 3.1. Двойственная задача линейного программирования
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. ОСНОВНЫЕ СПОСОБЫ ПЕРЕДВИЖЕНИЯ И ПРЕОДОЛЕНИЯ ПРЕПЯТСТВИЙ
  11. I. Открытые способы определения поставщика.
  12. I. Ситуационные задачи и тестовые задания.

Дана задача квадратичного программирования

 

(9.35)

 

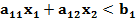
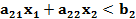
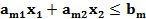
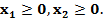
Линейная система ограничений описывает некоторую выпуклую многоугольную область на плоскости (. Множество всех точек X(, 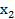), в которых целевая квадратичная функция принимает заданное значение , лежит на линии уровня данной функции. Эти линии являются кривыми, обрауземыми при пересечении поверхности (9.35) с плоскостью 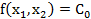. Форма этих кривых зависит от вида квадратичной функции.

 

Рассмотрим простейшие случаи:

1.

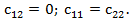
В этом случае линии уровня являются концентрическими окружностями. Чтобы определить центр этих окружностей, необходимо привести квадратичную функцию к виду

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)