Метод Гомори

К основной задаче ЛП добавим дополнительное условие – условие целочисленности неизвестных, в результате получим задачу ЛЦП. Можно, конечно, получить дробное оптимальное решение задачи ЛП и его округлить до ближайших целых значений. Но тогда может случиться, что мы будем либо близки к оптимальному плану задачи ЛЦП, либо далеки, либо вообще уйдем за пределы множества планов ЛЦП. Один из возможных методов решения задачи ЛЦП – метод Гомори. Идея метода базируется на представлении вещественного числа в виде суммы его целой и дробной частей. Как известно, целой частью вещественного числа «а» называется наибольшее целое число, не превосходящее Обозначение целой части [a]. 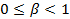Разность есть дробная часть числа Очевидно, например, что и 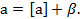Например:

Рассмотрим метод Гомори на примере (общая задача ЛП):

План задачи линейного программирования называют целочисленным, если все его составляющие целые числа.

Для определения целочисленного решения задачи:

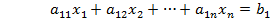
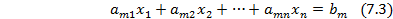
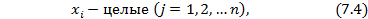
или в краткой форме:

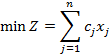
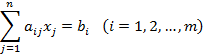
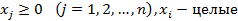
можно использовать алгоритм Гомори, состоящий из следующих этапов.

Первый этап. Задача (7.1) - (7.3) решается симплекс-методом до получения оптимального плана.

Второй этап. В последнюю симплекс-таблицу, содержащую оптимальный план, добавляют ограничение

составленное для i - ой строки следующим образом:

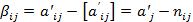
где

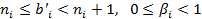
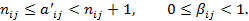
(Символом [ a ] обозначают целую часть числа a, то есть наибольшее целое число, не превосходящее a).

Третий этап. В последней симплекс-таблице выбирают введенную строку разрешающей. Разрешающий столбец выбирают по правилу двойственного симплекс-метода. С выбранным таким образом разрешающим элементом осуществляют переход по известному алгоритму к следующей симплекс-таблице. Если при этом полученное решение окажется еще не целочисленным, то общий шаг повторяют.

Поиск по сайту: