 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Симметричные двойственные задачи
Задача об использовании сырья [4, стр.4, 38].
Из сырья I и II (например: мука и вода), запасы которого ограничены и составляют 60 и 45 единиц соответственно, изготавливается продукция 3-х видов. На производство единицы продукции 1 го вида затрачивается 4 ед. сырья I и 2 ед. сырья II; 2 го вида – 2 и 6 соответственно, а 3 го вида – 6 и 4 ед. Выручка от производства единицы продукции каждого вида составляет соответственно 12 руб., 15руб., 19руб. Надо найти такой план выпуска продукции, при котором сырье не будет перерасходовано, а суммарная выручка будет наибольшей.
| Сырье | Затраты сырья на единицу продукции вида | Запасы сырья | ||
| I | ||||
| II | ||||
| Выручка за ед. продукции (руб) |
Пусть:
x1 – количество единиц выпущенной продукции 1-го вида;
x2 – количество единиц выпущенной продукции 2-го вида;
x3 – количество единиц выпущенной продукции 3-го вида.
Тогда можно записать:
Вводим искусственный базис 
Исходная таблица
| В | Св. член | Коэффициент при неизвестных | ||||
| 
| 
| 
| 
| ||
| ||||||
|
| ||||||
| -12 | -15 | -19 |
Итерация 1
| В | Св. член | Коэффициент при неизвестных | ||||
| 
|
|
|
| ||
|
| 1/2 | 3/2 | 1/4 | |||
| - 1/2 | |||||
|
| - 9 | - 1 |
Итерация 2
| В | Св. член | Коэффициент при неизвестных | ||||
|
|
|
|
|
| ||
|
| 27/2 | 7/5 | 3/10 | -1/10 | ||
|
| 1/5 | -1/10 | 1/5 | |||
|
| 4/5 | 21/10 | 9/5 |
Ответ: 
= 13,5 единиц
= 3 единицы
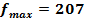руб.
Для получения максимальной выручки 207 руб., надо выпустить 13,5 ед. продукции 1-го вида и 3 ед. 2-го вида, значение 
= 0 означает, что продукцию 3-го вида выпускать не следует.
Поставим своей целью назначить «справедливые» продажные цены на оба сырья. Пусть, например, 
- цена единицы I-го сырья, 
цена единицы II-го сырья. Тогда стоимость всего сырья 
. Общая задача ЛП имеет вид:
Любое решение задачи (2) называется планом оценок ресурсов, а оптимальный план – оптимальные оценки. Разумеется, оптимальные оценки ресурсов, определенные в условиях данной задачи имеют относительный смысл. В условиях другой задачи те же ресурсы могут иметь другие оценки.
.
Или после тождественных преобразований (вычитаем из третьего уравнения первое и второе и меняем знаки) система примет следующий вид:
Формулируем задачу минимизации:
Исходная таблица
0 0 0 0 0 0 1
| В | Св. член | Коэффициент при неизвестных | |||||
 ↓
| 
| 
| 
| 
| 
| ||
| 0
| -1 | ||||||
⟶0 
| -2 | -1 | |||||
| 1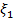
| -1 | ||||||
| -1 |
Итерация 1
| В | Св. член | Коэффициент при неизвестных | |||||
|
|
|
|
|  ↓
|
| ||
|
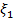
| -1/2 | -1/2 | |||||
|
| -1/2 | 1/4 | -1/4 | ||||
| -3/2 | 1/2 | |||||
|
| -3/2 | 1/2 |
Итерация 2
| В | Св. член | Коэффициент при неизвестных | |||||
|
|
|
|
|
|
| ||
|
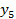
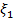
| -2 | ||||||
|
| 15/2 | -2/4 | 1/2 | ||||
|
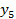
| -3 | ||||||
|
| -1 |
Исходная таблица
| В | Св. член | Коэффициент при неизвестных | ||||
|
|  ↓
|
|
|
| ||
|
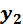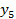
| 7,5 | -1/2 | ||||
| -2 | |||||
|
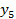
| -3 | |||||
| -30 |
Итерация 1
| В | Св. член | Коэффициент при неизвестных | ||||
|
|
|
|
|
| ||
|
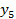
| 2,1 | |||||
|
| 1,8 | 1/10 | -2/10 | |||
|
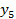
| 0,8 | |||||
|
| -13,5 | -3 |
Ответ: 
= 2,1 руб.; 
= 1,8 руб. – оптимальные оценки ресурсов. 
= 
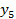, =0,8 руб.
Вывод: Для получения «справедливой» продажной стоимости сырья надо назначить цены за единицу I сырья – 2,1 руб.; за единицу II сырья – 1,8 руб. Равенства = означает, что продажная стоимость сырья равна выручке от продажи единицы продукции 1 и 2 видов; 
= 0,8 руб. означает, что продажная стоимость сырья на изготовление единицы продукции 3-го вида на 0,8 руб. больше выручки. Минимальная продажная стоимость всего сырья в задаче (2) = максимуму выручки в задаче (1).
Поиск по сайту: