 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Если после выполнения очередной итерации задачи
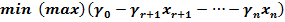
при условиях:
;
.
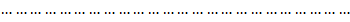
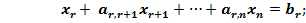
1) найдется хотя бы одна положительная (отрицательная) оценка и в каждом столбце с такой оценкой найдется хотя бы один положительный элемент, то можно улучшить решение, выполнив следующую итерацию;
2) найдется хотя бы одна положительная (отрицательная) оценка, столбец которой не содержит ни одного положительного элемента, то функция не ограничена в области допустимых решений;
3) все оценки окажутся отрицательными (положительными), то достигнуто оптимальное решение.
§ 4. Решение почти канонических задач.
Если система уравнений каноническая, а в выражении для целевой функции есть базисные переменные, то задача ЛП будет иметь почти канонический вид.
Пример:
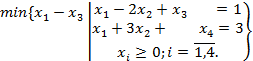
Здесь переменные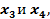 
являются базисными, а 
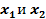– свободными переменными. Так как базисное переменное 
входит в выражение для целевой функции, а система уравнений каноническая, то эта задача является почти канонической. Для ее решения симплексным методом необходим переход к каноническому виду. Для этого надо базисные переменные, входящие в целевую функцию (в нашем случае базисное переменное 
), выразить через свободные переменные (т.е.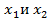 
). Из первого уравнения системы имеем 
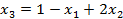. Тогда целевая функция примет вид 
. Решаем теперь уже каноническую задачу.
.
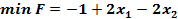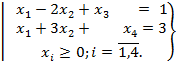
Запишем исходную симплексную таблицу и решение задачи.
Исходная симплексная таблица
0 1 0 -1 0
| 
| Коэффициенты при неизвестных | ||||
|  ↓
|
| 
| |||
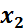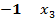
| -2 | |||||
| 0 →x4 | ||||||
| F | -1 | - 2 | ||||
Итерация 1
|
|
| Коэффициенты при неизвестных | |||
|
| 
|
|
| ||
|
| 5/3 | 2/3 | |||
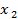
| 1/3 | 1/3 | |||
| F | -3 | -8/3 | -2/3 |
Оптимальное решение: (0,1,3,0);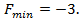 
При решении почти канонических задач существует правило заполнения индексной строки, которое делает излишним предварительные алгебраические преобразования целевой функции [4]. Например,
минимизировать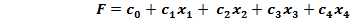 
при условиях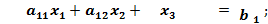 
.
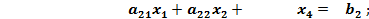
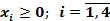Исходная симплексная таблица записывается следующим образом:
| 
| 
| 
| 
| |
|
|
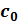
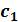
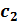
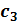
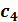
| Коэффициенты при неизвестных | |||
|
|
|
|
| ||
| 
| 
| 
| 
| |
| 
| 
| 
| ||
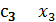
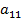
| F |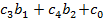 
| 
| 
|
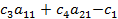
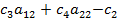
Соответственно в нашем числовом примере коэффициенты индексной строки (см. исходные симплексные таблицы)
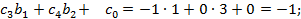
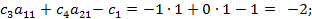
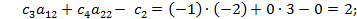
Поиск по сайту: