Чувствительность оптимума

Решение оптимальной задачи, полученное с использованием математической модели процесса, всегда дает лишь идеализированное представление об оптимальном режиме реального процесса, так как никакая модель не может полностью заменить оптимизируемый объект. Кроме того, при применении такого режима неизбежны отклонения от найденного закона оптимального управления. Поэтому, прежде чем перейти к вопросам практической реализации оптимального режима, интересно хотя бы приближенно оценить чувствительность найденного оптимального решения к изменению параметров, модели в частности, к изменению управляющих действий. Под чувствительностью оптимума ниже будет пониматься относительное изменение критерия оптимальности при отклонении управляющих воздействий от оптимальных значений. Вообще говоря, в приведенное определение чувствительности оптимума следует включить не только зависимость критерия от управляющих воздействий, но также и от всех остальных параметров математической модели, для которых в процессе моделирования необходимо задавать численные значения. В этом случае постановка задачи исследования чувствительности оптимума найденного на математической модели процесса, окажется наиболее полной. Однако принципиально анализ чувствительности оптимума несмотря на то, по какому параметру ее исследуют, проводят аналогичным методами. Поэтому в дальнейшем ограничимся рассмотрением чувствительности только по отношению к управляющим воздействиям. Предположим, что известно оптимальное управление (i= 1,..., r), максимизирующее значение критерия оптимальности R, который при этом принимается только как функция управляющих воздействий:

R = R (,…, ) (1,33)

При отклонении управляющих воздействий от оптимальных знаний на величины изменение критерия оптимальности определяется выражением:

𝜟R=R(,…, +𝜟 )- R(,…, 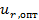) (1,34)

Для малых значений 𝜟 оценка изменения критерия оптимальности может быть получена разложением правой части выражения (I,34) в ряде по степеням 𝜟 с точностью до членов второго порядка малости:

𝜟R= 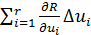+ (1,35)

=0 i = 1,…,r (1,36)

С учетом равенства (1,36) выражение для оценки изменения критерия оптимальности можно записать в виде:

(1,37)

Допустим, что максимальное отклонение управляющих воздей­ствий от оптимального значения не превышает величины . В дан­ном случае может быть принято неравенств

I, k=1,…,r (1, 38)

Комбинируя выражения (1,37) и (1,38), получим следующую оценку для изменения критерия оптимальности:

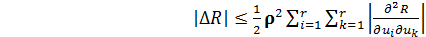где производные суммируют по модулю для того, чтобы учесть воз­можное различие их знаков. Для оценки размеров окрестности _м, в которой допустимо из­менение значений управляющих воздействий при изменении крите­рия оптимальности не более чем на из выражения (1,39) получим формулу

, (1,40)

которая для одного управляющего воздействия имеет простой вид:

(1,41)

Специфической особенностью методов решения оптимальных задач (за исключением методов нелинейного программирования) является то, что до некоторого этапа оптимальную задачу решают аналитически, т. е. находят определенные аналитические выраже­ния, например, системы конечных или дифференциальных уравне­ний, откуда уже отыскивают оптимальное решение. В отличие от указанных методов при использовании методов нелинейного про­граммирования, которые, как уже отмечалось выше, могут быть названы прямыми, применяют информацию, получаемую при вы­числении критерия оптимальности, изменение которого служит оценкой эффективности того или иного действия. Важной характеристикой любой оптимальной задачи является ее размерность п, равная числу переменных, задание значений ко­торых необходимо для однозначного определения состояния опти­мизируемого объекта. Как правило, решение задач высокой раз­мерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программиро­вание и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерно­сти, которые могут быть представлены как многостадийные про­цессы с относительно невысокой размерностью каждой стадии.

Поиск по сайту: